发表更新编译器24 分钟读完 (大约3570个字)0次访问

课程笔记：AI 编译器前端优化 | 编译器

本文是以下教学视频的笔记：【AI编译器】系列之前端优化

概述

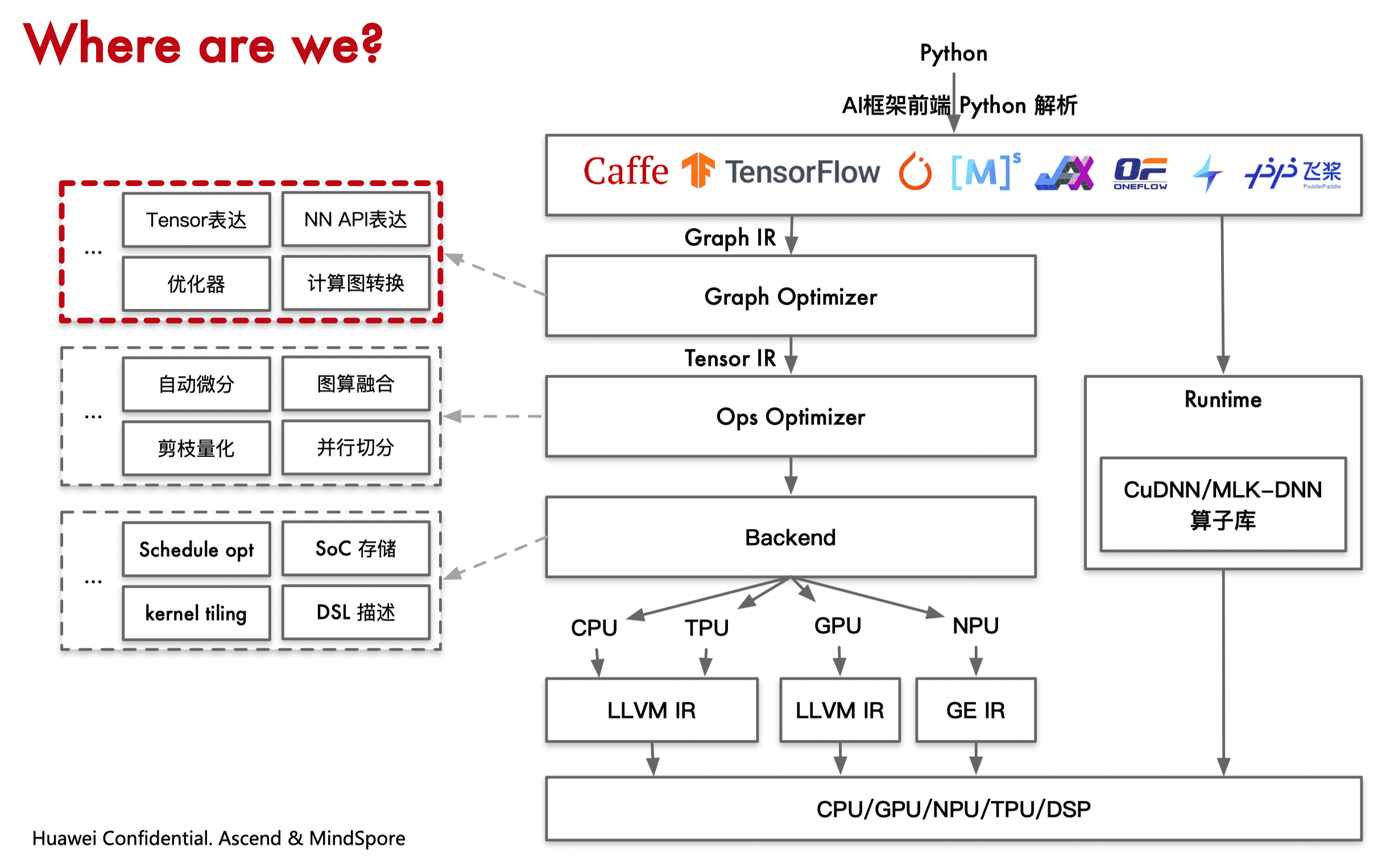
算子融合（OP Fusion）

融合方式

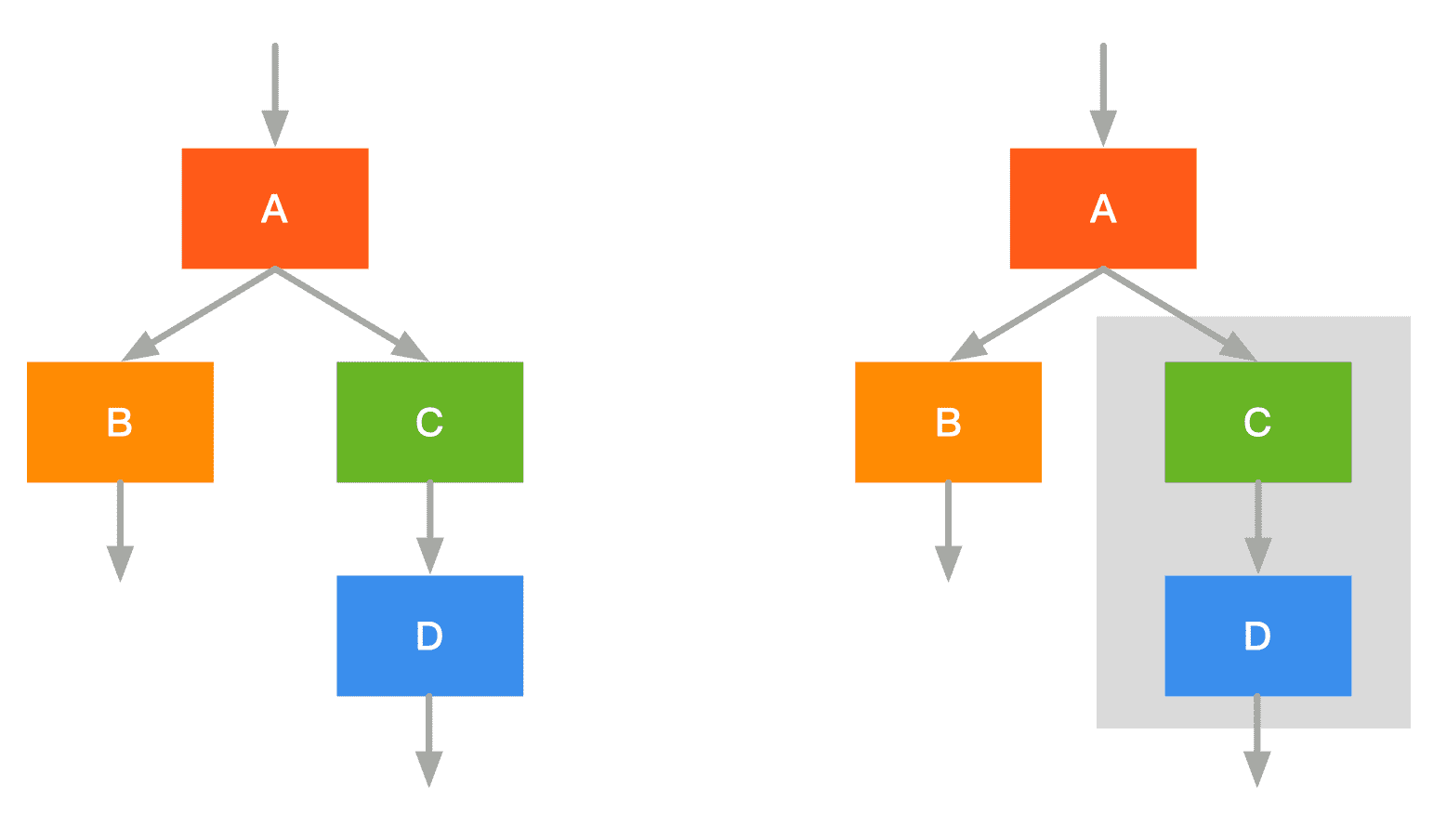
  • 融合前：启动 CD 两个 kernel
  • 融合后：启动 C+D 一个 kernel

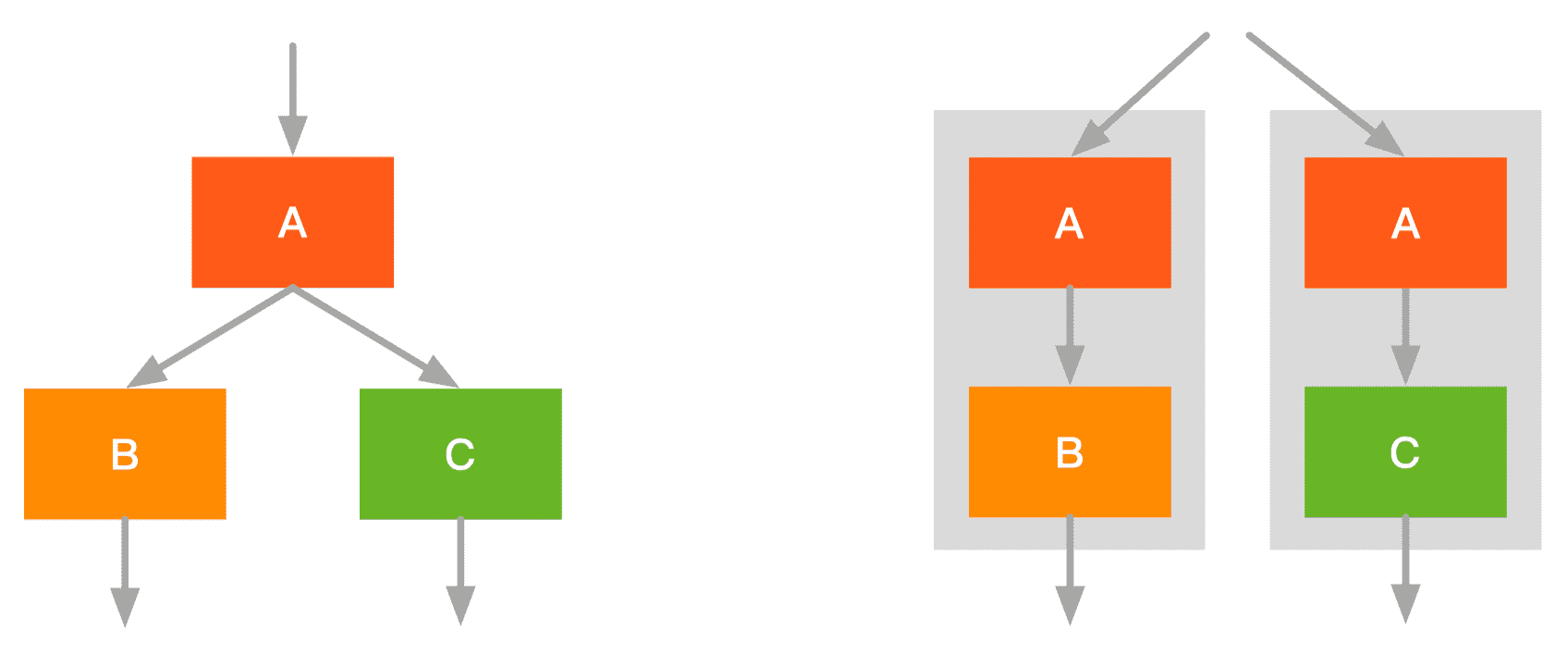
  • 融合前：启动 A 一个 kernel，并发 B/C 各自启动一个 kernel
  • 融合后：并发 A+B/A+C 各自启动一个 kernel

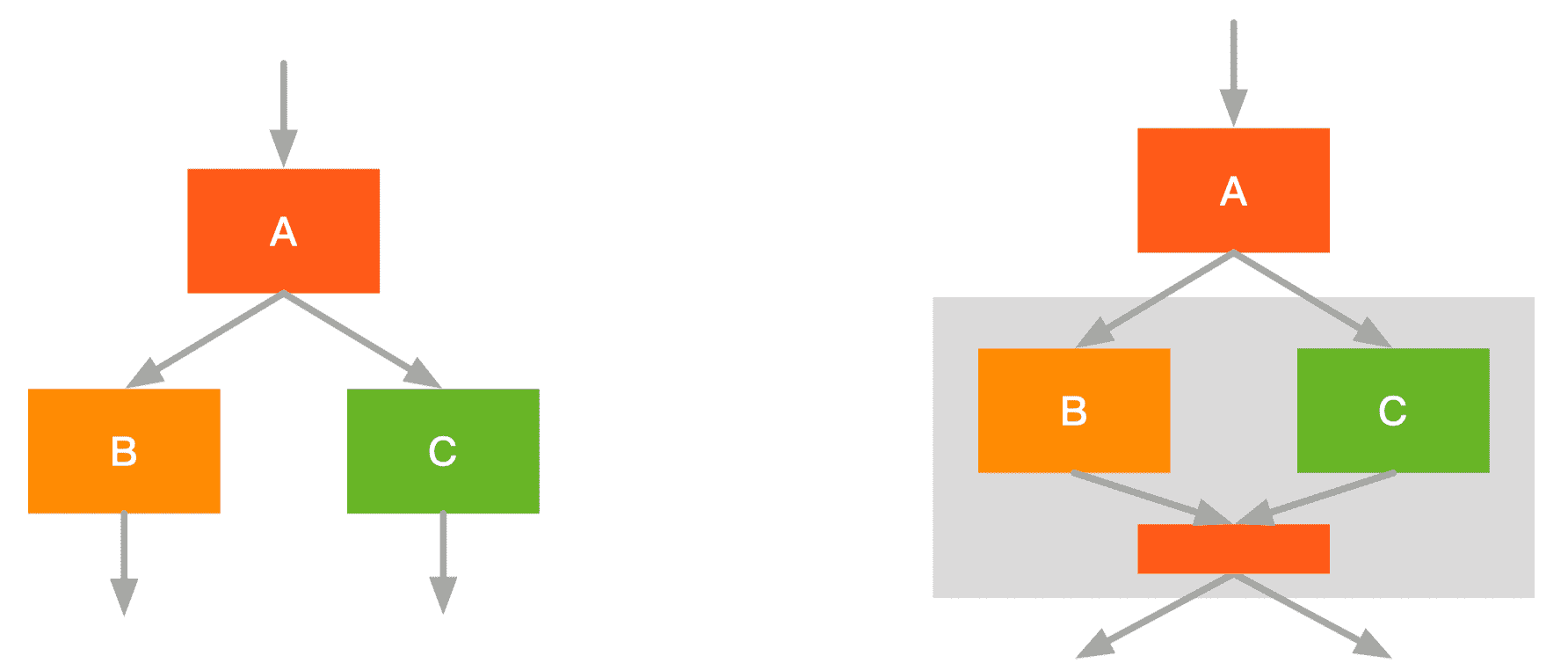
  • 融合前：启动 A 一个 kernel，并发 B/C 各自启动一个 kernel
  • 融合后：BC融合，减少一次 kernel 调用；两者的结果放进同一块内存，访存效率更高

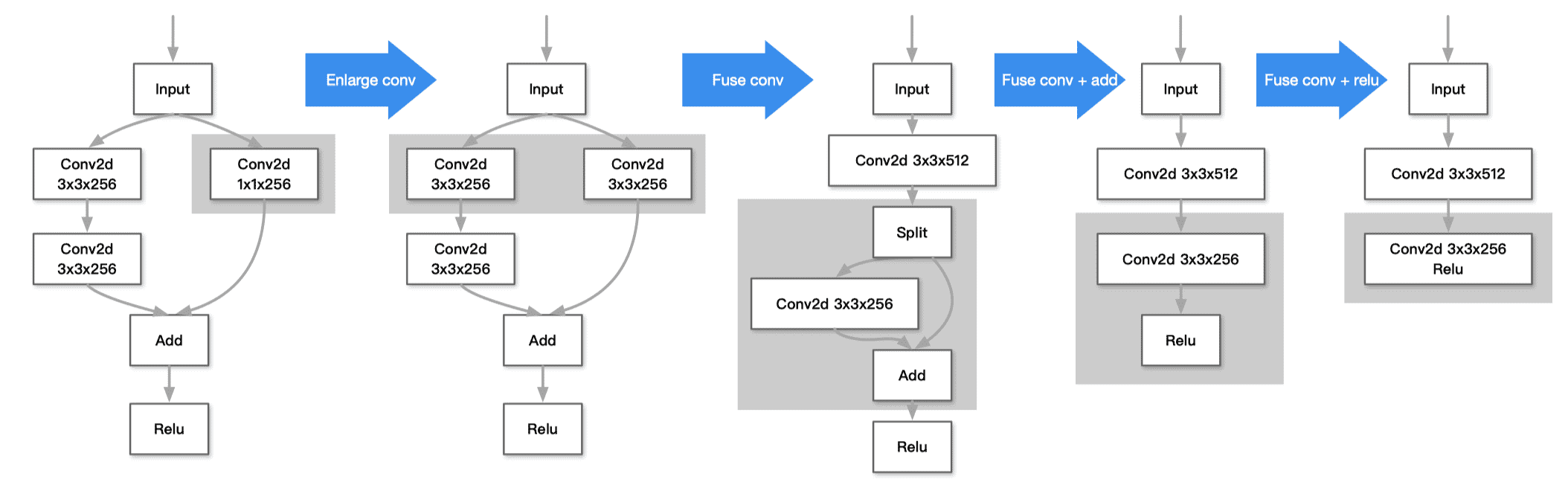
  • 融合前：多算子
  • 融合后：算子减少了很多，部分计算可能会变大，总体来说减少了访存的开销

融合算子出现主要解决模型训练过程中的读入数据量，同时减少中间结果的写回操作，降低访存操作。具体来说，解决以下两个问题：

  • 内存墙：主要是访存瓶颈引起。算子融合主要通过对计算图上存在数据依赖的“生产者-消费者”算子进行融合，从而提升中间 Tensor 数据的访存局部性，以此来解决内存墙问题。这种融合技术也统称为“Buffer 融合”。在很长一段时间，Buffer 融合一直是算子融合的主流技术。早期的 AI 框架，主要通过手工方式实现固定 Pattern 的 Buffer 融合。
  • 并行墙：主要是由于芯片多核增加与单算子多核并行度不匹配引起。可以将计算图中的算子节点进行并行编排，从而提升整体计算并行度。特别是对于网络中存在可并行的分支节点，这种方式可以获得较好的并行加速效果。

TVM 支配树

TVM 整体的算子融合是基于支配树实现的，支配树就是由各个点的支配点构成的树，支配点是所有能够到达当前节点的路径的公共祖先点（Least Common Ancestors，LCA）。

对于一张有向图（可以有环）我们规定一个起点 r, 从 r 点到图上另一个点 w 可能存在很多条路径。如果对于 r->w 的任意一条路径中都存在一个点 p, 那么我们称点 p 为 w 的支配点（也可以称作是 r->w 的必经点）。

TVM 的算子融合策略就是检查每个 node 到其支配点的所有 node 构成的集合是否符合融合规则，如果符合就对其进行融合。基于支配树进行判断可以保证融合掉的 node 节点不会对剩下的节点产生影响。

参考：【从零开始学深度学习编译器】八，TVM的算符融合以及如何使用TVM Pass Infra自定义Pass

TVM 算子融合规则

  • injective(one-to-one map)：映射函数，如加法、点乘等
  • reduction：约简函数，如 sum/max/min，输入到输出具有降维性质的，如 sum
  • complex-out-fusable(can fuse element-wise map to output：人工定义的计算比较复杂的 pattern，如 conv2d
  • opaque(cannot be fused)：无法被融合的算符，如 sort

布局转换（Layout Transform）

数据内存排布

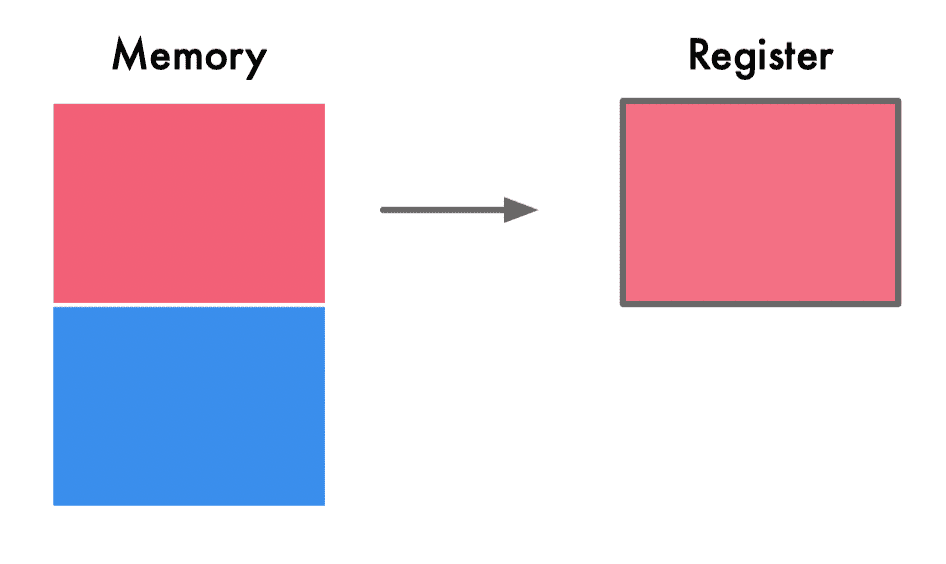
没有进行内存对齐：

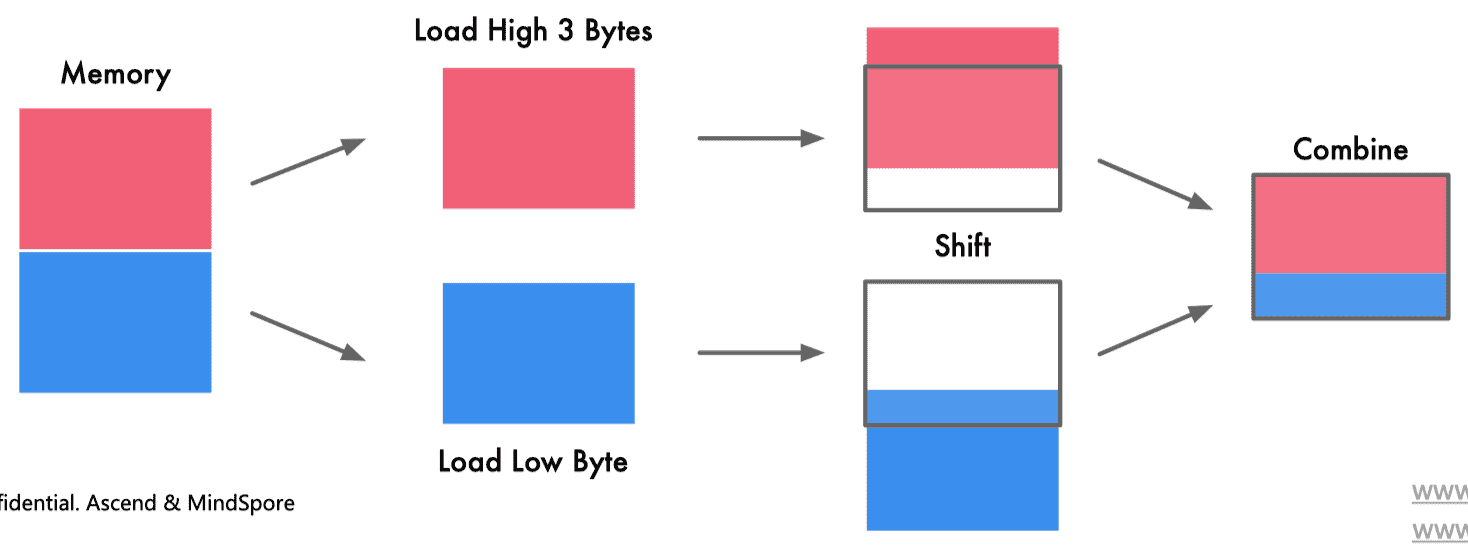
进行了内存对齐：

进行内存对齐主要有以下两个方面好处：

  • 访问速度：CPU 总是以其字的大小进行内存读取，进行未对齐的内存访问时，处理器将读取多个字，需要读取变量所跨越内存的所有字，同时进行处理。将导致访问请求数据所需要的内存事务增加 2 倍
  • 原子性：CPU 可以在一个对齐的内存字上操作，意味着没有指令可以中断该操作。这对于许多无锁数据结构和其他并发范式的正确性至关重要

张量数据布局

NCHW

  • 同一个通道的数据值连续排布，更适合需要对每个通道单独运算的操作，如 MaxPooling
  • 需要将整个通道都放到内存中，计算时需要的存储更多，适合 GPU 运算，利用 GPU 内存带宽较大并且并行性强的特点，其访存与计算的控制逻辑相对简单

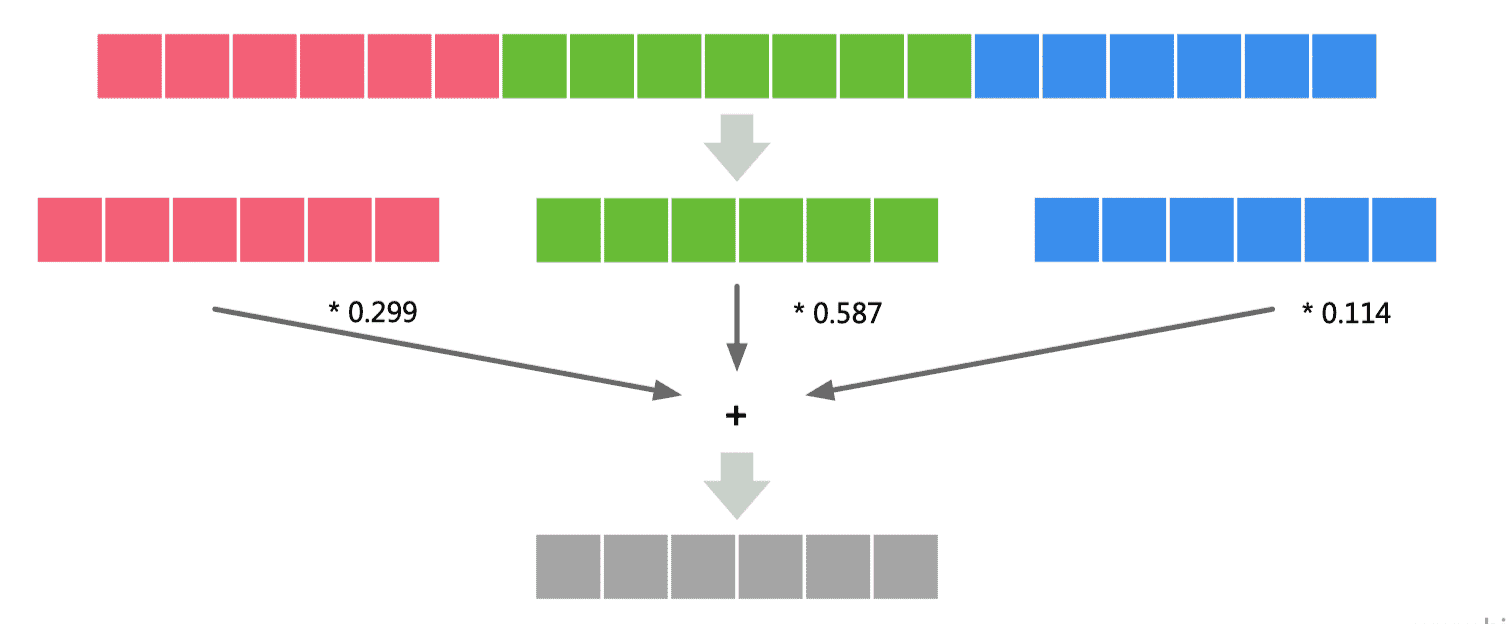
NHWC

  • 不同通道中的同一位置元素顺序存储，因此更适合那些需要对不同通道的同一数据做某种运算的操作，比如 Conv1x1
  • 适合多核 CPU 运算，CPU 内存带宽相对较小，每个数据计算的时延较低，临时空间也很小，有时计算机采取异步的方式边读边算来减小访存时间，因此计算控制灵活且复杂

编译布局转换优化

  • 目的：将内部数据布局转化为后端设备友好的形式
  • 方式：试图找到在计算图中存储张量的最佳数据布局，然后将布局转换节点插入到图中
  • 注意：张量数据布局对最终性能有很大的影响，而且转换操作也有很大的开销

NCHW 格式操作在 GPU 上通常运行得更快，所以在 GPU 上转换为 NCHW 格式是非常有效。一些 AI 编译器依赖于特定于硬件的库来实现更高的性能，而这些库可能需要特定的布局。此外，一些 AI 加速器更倾向于复杂的布局。边缘设备通常配备异构计算单元，不同的单元可能需要不同的数据布局以更好地利用数据，因此布局转换需要仔细考虑。AI 编译器需要提供一种跨各种硬件执行布局转换的方法。

内存分配（Memory Allocation）

Inplace operation：如果一块内存不再需要，且下一个操作是 element-wise，可以原地覆盖内存。

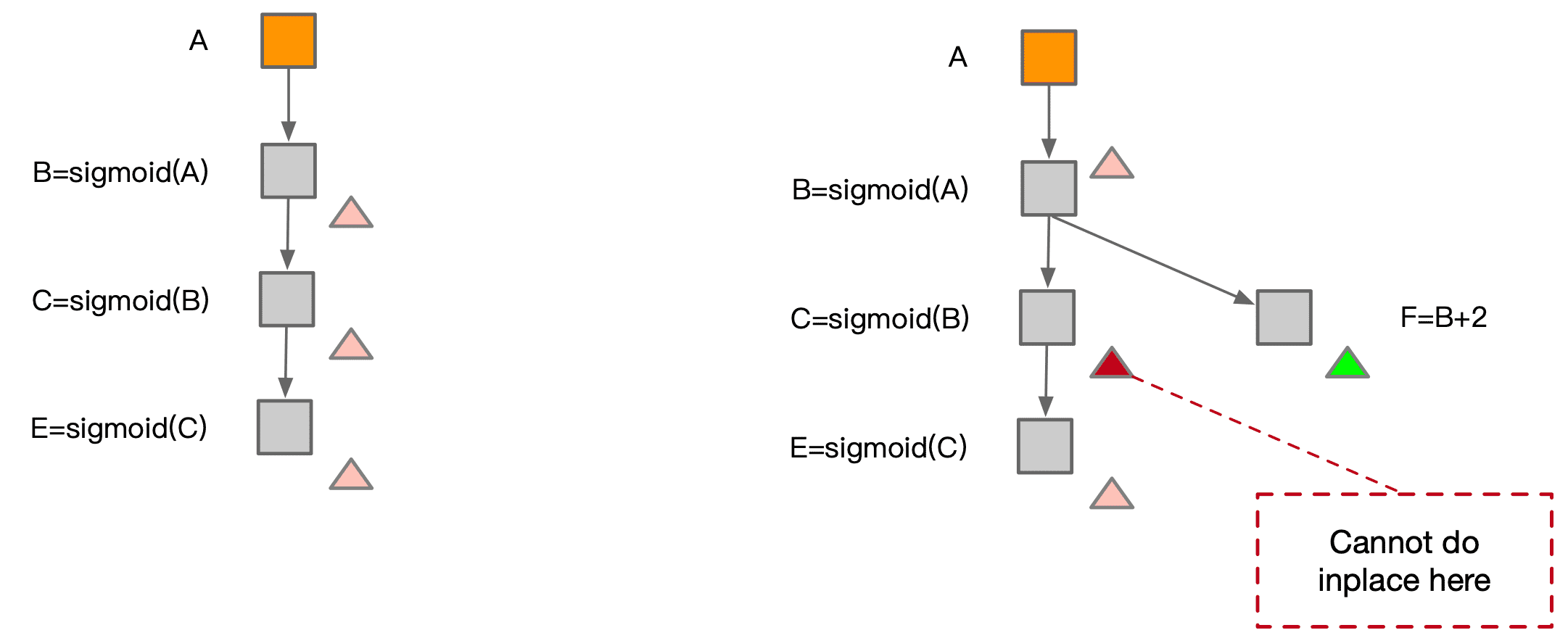
Memory sharing：两个数据使用内存大小相同，且有一个数据参与计算后不再需要，后一个数据可以覆盖前一个数据。

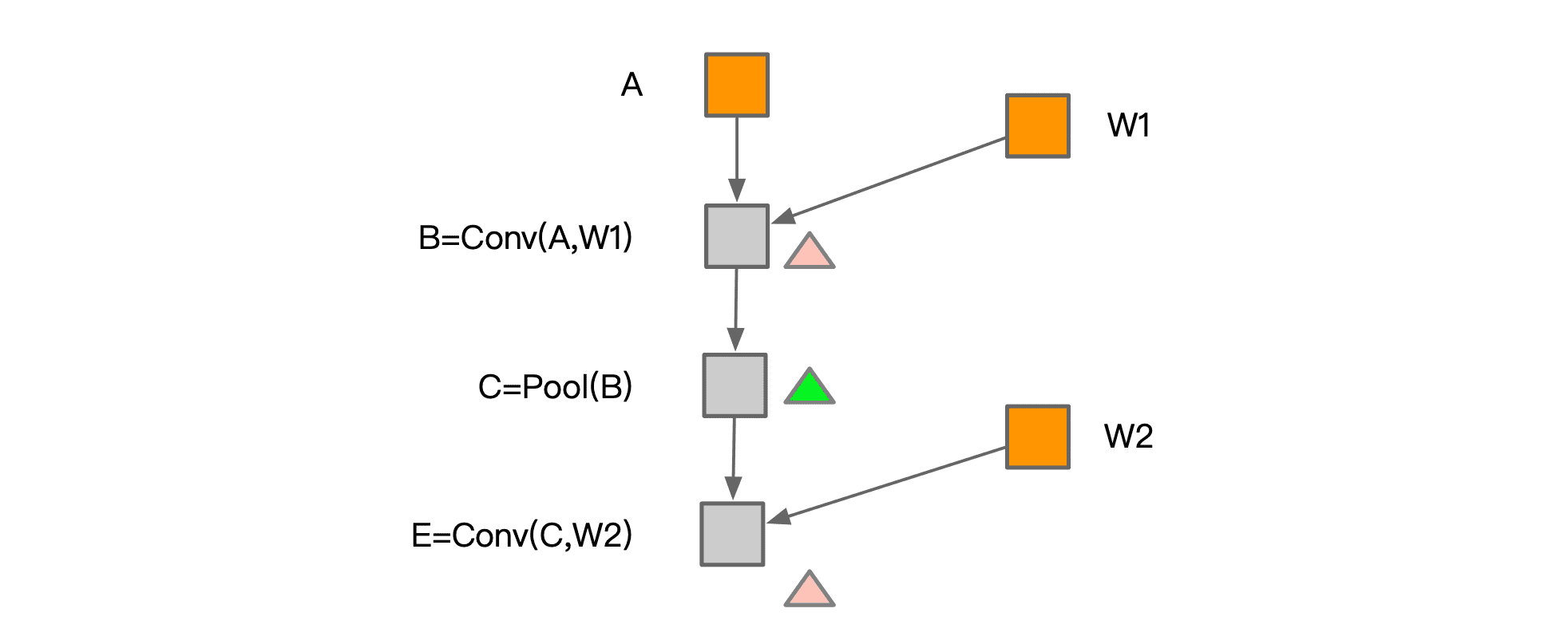
两者结合起来，在训练场景的应用如下：

整体思路与传统编译器寄存器分配非常相似。

常量折叠（Constant Fold）

常量折叠与常量传播

常量折叠（constant fold）：通过对编译时常量或常量表达式进行计算来简化代码。

1
i = 320 * 200 * 32
1
2
3
4
5
%a: load 320
%b: load 200
%x: mul %a, %b
%c: load 32
%y：mul %x, %c
1
%a: load 2048000

常量传播（constant propagation）：可以在一段代码中，将表达式中的常量替换为相关表达式或字面量，再使用常量折叠技术来简化代码。

1
2
3
4
def foo():
    x = 14
    y = 7 - x / 2
    return y * (28 / x + 2)
1
2
3
4
def foo():
    x = 14
    y = 7 - 14 / 2
    return y * (28 / 14 + 2)

AI 编译器中的常量折叠

BN 折叠

在推理时，BN 层的公式如下：

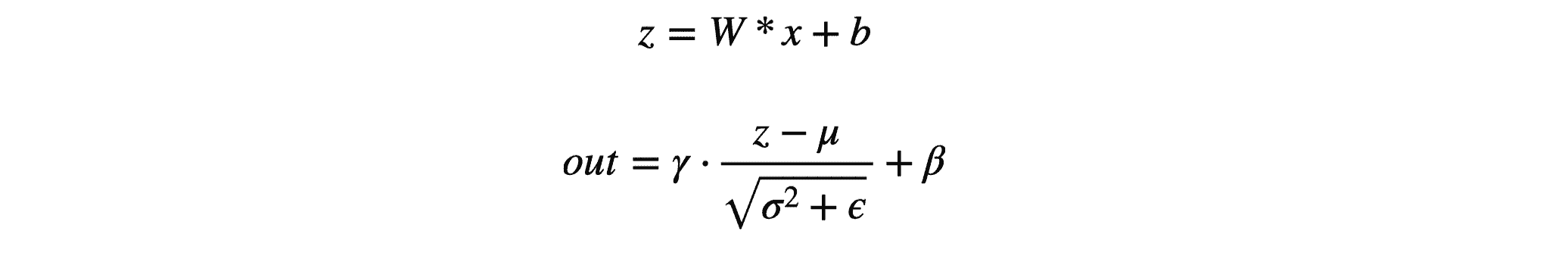
进行简单变换后可以表示为：

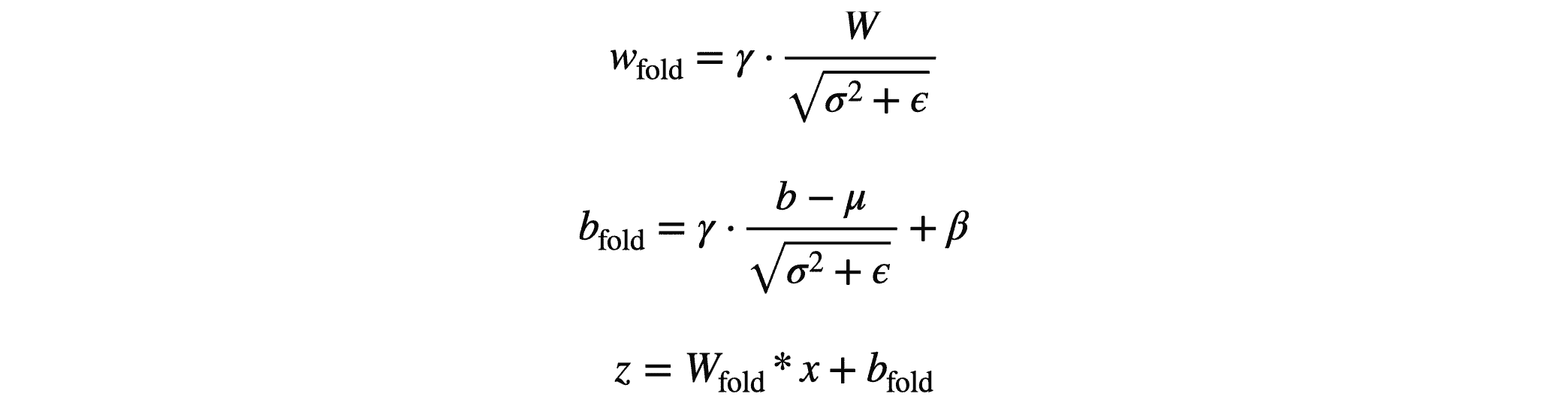
此时 $w_{fold}$ 和 $b_{fold}$ 均为常量，BN 就像是对上一层的结果进行简单的线性转换。

公共子表达式消除（CSE）

CSE

CSE（Common subexpression elimination）是一个编译器优化技术。在执行这项优化的过程中，编译器会视情况将多个相同的表达式替换成一个变量，这个变量存储着计算该表达式后所得到的值。

1
2
a = b * c + g
d = b * c + e

可以观察到 b * c 是两项表达式中的公共子表达式。则可以将以上代码转换成以下代码：

1
2
3
tmp = b * c
a = tmp + g
d = tmp + e

执行这项优化的可能性基于表达式的定义可达性。当以下条件成立，则一个表达式 b * c 在程序的某个点 p 被定义为是可达的：

  • 从初始节点到点 p 的每条路径在到达 p 之前计算过 b * c
  • b * c 被计算后，无论 b 或者 c 到达 p 以前都没有被重新赋值过

由编译器计算的成本效益分析可以判断出，重复计算该表达式的开销是否大于存储该表达式的计算结果，并且这个分析也要将寄存器等因素考虑在内。

AI 编译器中的 CSE

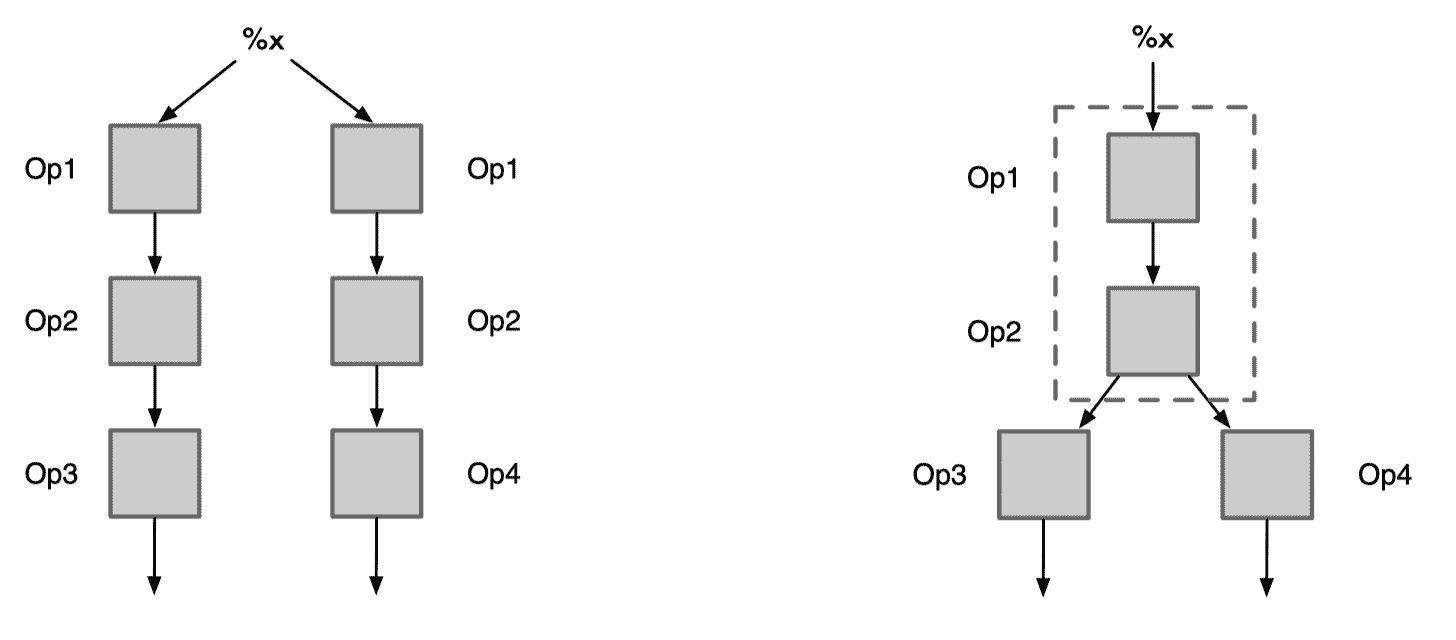
  1. 获取逆后序节点集 Set(Reverse)：对计算图 Graph IR 进行深度优先遍历，将结果逆转得到逆后序节点集。逆后序得到的结果就是拓扑排序，即访问到某一个节点时，该节点的依赖节点都已经被访问。

  2. 创建 Map(MSE)：存储公共子表达式候选集，遍历 Set(Reverse) 时，可以从候选集 Map(MSE) 中查找是否有可以使用的表达式。

  3. 遍历计算图的所有节点，判断是否有公共子表达式：获取节点 hash 值，hash 的 key 由输出个数 + 输出类型 s + 输入节点 id，key 可以保证输入相同及输出个数和类型相同时，得到的 hash 值相同，达到检索公共表达式的目的。

  4. 记录入候选集：根据 hash 值 h 从 Map(MSE) 中得到候选集，当候选集为空，第一次遇到这样的表达式，将节点 Node 存入 Map(MSE) 中。

  5. 可复用公共子表达式判断：candidate 非空，则说明之前遍历到了相似的表达式，进一步判断是否可复用已保存节点表达式的结果：节点的输入都是来自相同的 const 节点，可以保证输入数据完全相同；输出个数和类型相同，可以保证输出的结果相同；满足条件下，可复用之前保存节点的结果，不用再次进行计算。

  6. 删除重复节点：判断表达式可以复用后，最后一步就是删除重复的节点，将 candidate 的输出连接到当前节点的输出节点对应的输入，最后删除当前节点。

死代码消除（DCE）

死代码消除可以优化计算图的计算和存储效率，避免为死节点（无用节点）分配存储和进行计算，同时简化了计算图的结构，方便进行后续的其他图优化 pass。

死代码消除一般不是在定义神经网络模型结构时候引起的，而是其他图优化 pass 造成的结果，因此死代码消除 pass 常常在其他图优化 pass 后被应用。

2023-01-02-n2OsS2

  1. 获取逆后序节点集 Set(Reverse)：对计算图 Graph IR 进行深度优先遍历，将结果逆转得到逆后序节点集。逆后序得到的结果就是拓扑排序，即访问到某一个节点时，该节点的依赖节点都已经被访问。

  2. 遍历后序节点集，判断是否为死节点：获取节点的输出值，判断是否为计算图的输出节点；如果不是输出节点且无对应输入节点，则为死节点。

  3. 删除死节点，重新遍历计算图：删除死节点，值得注意的是死节点删除后需要删除对应输入的边。然后重复步骤 1、2。

代数简化（ARM）

代数化简的目的是利用交换率、结合律等规律调整图中算子的执行顺序，或者删除不必要的算子，以提高图整体的计算效率。代数化简可以通过子图替换的方式完成，具体实现：

  • 可以先抽象出一套通用的子图替换框架，再对各规则实例化
  • 可以针对每一个具体的规则实现专门的优化逻辑

算术化简

通过利用代数之间算术运算法则，在计算图中可以确定优化的运算符执行顺序，从而用新的运算符替换原有复杂的运算符组合。

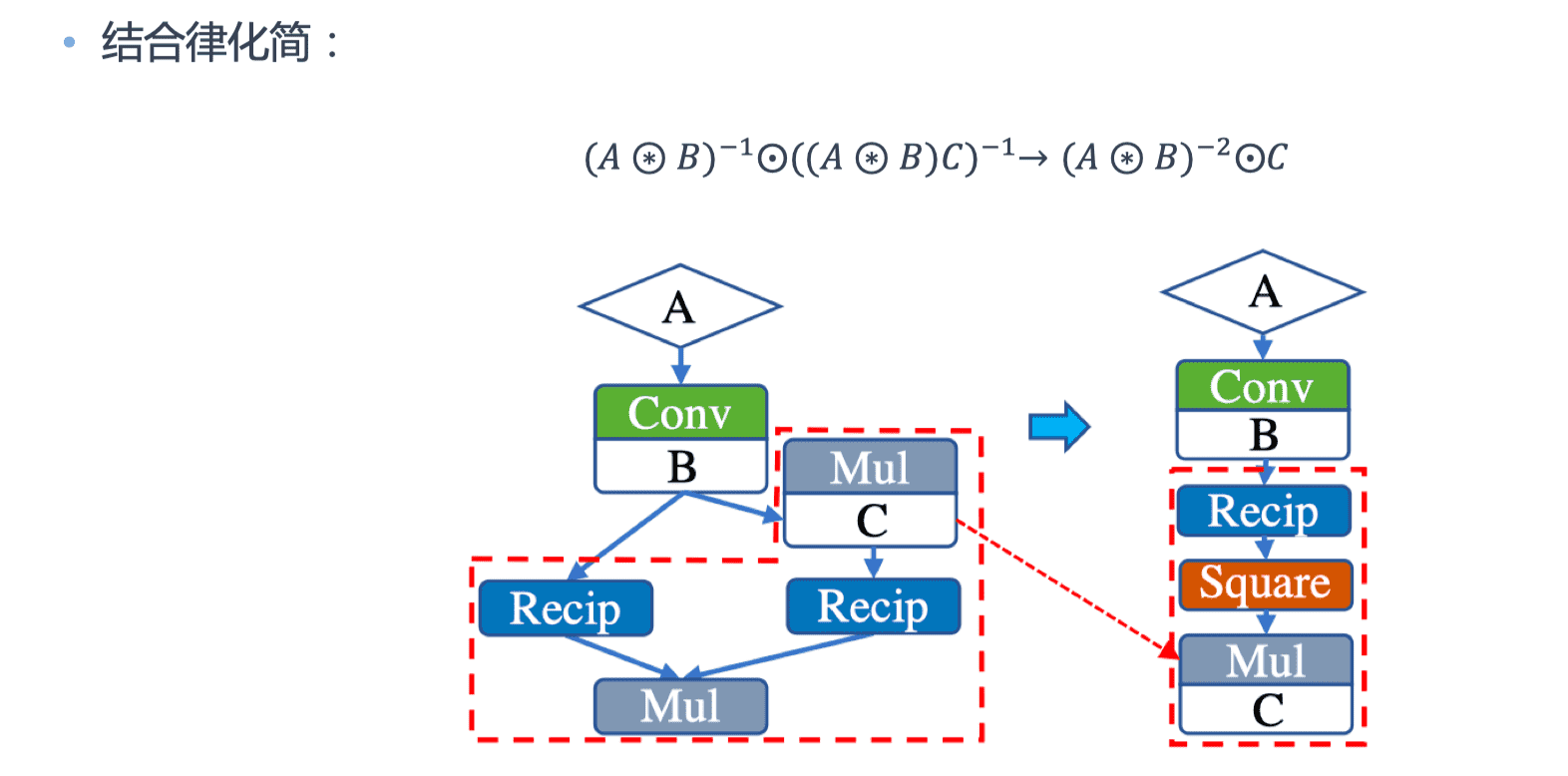
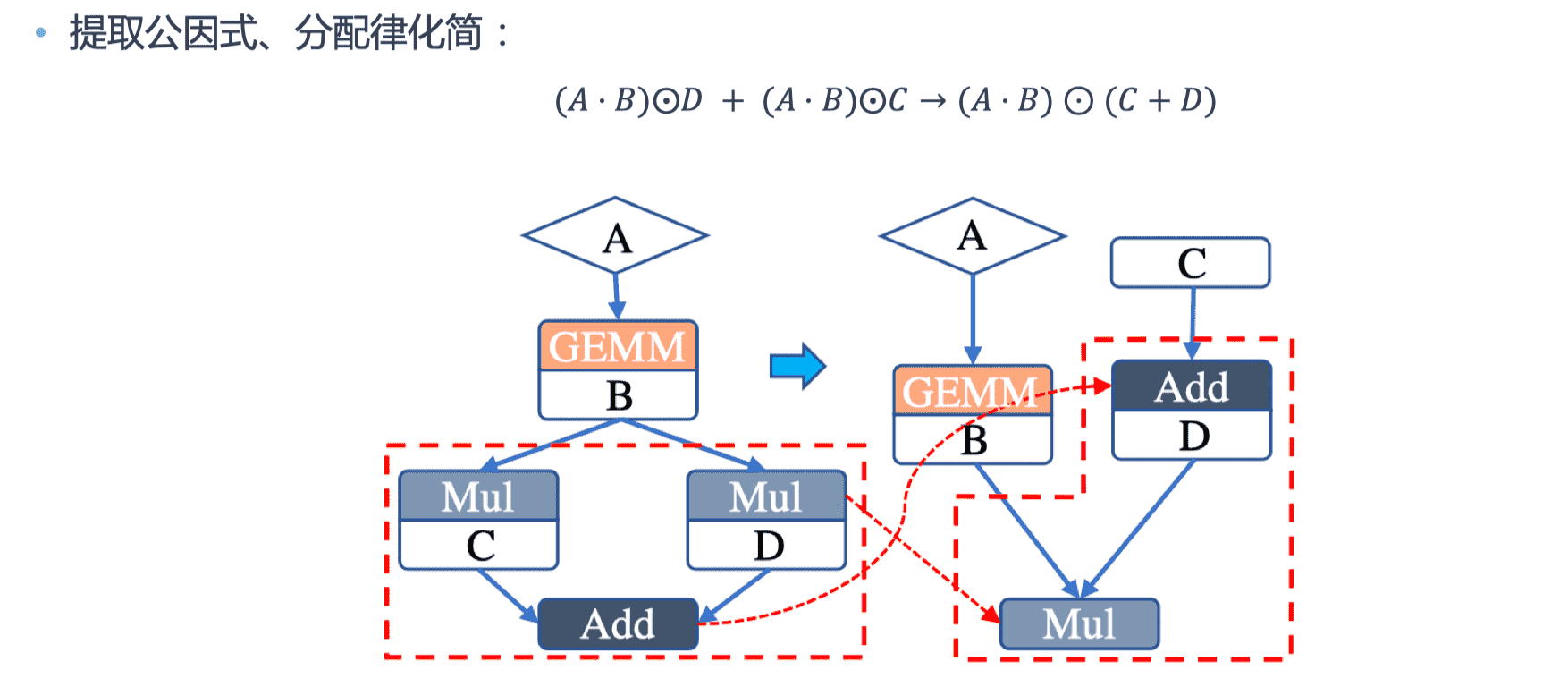
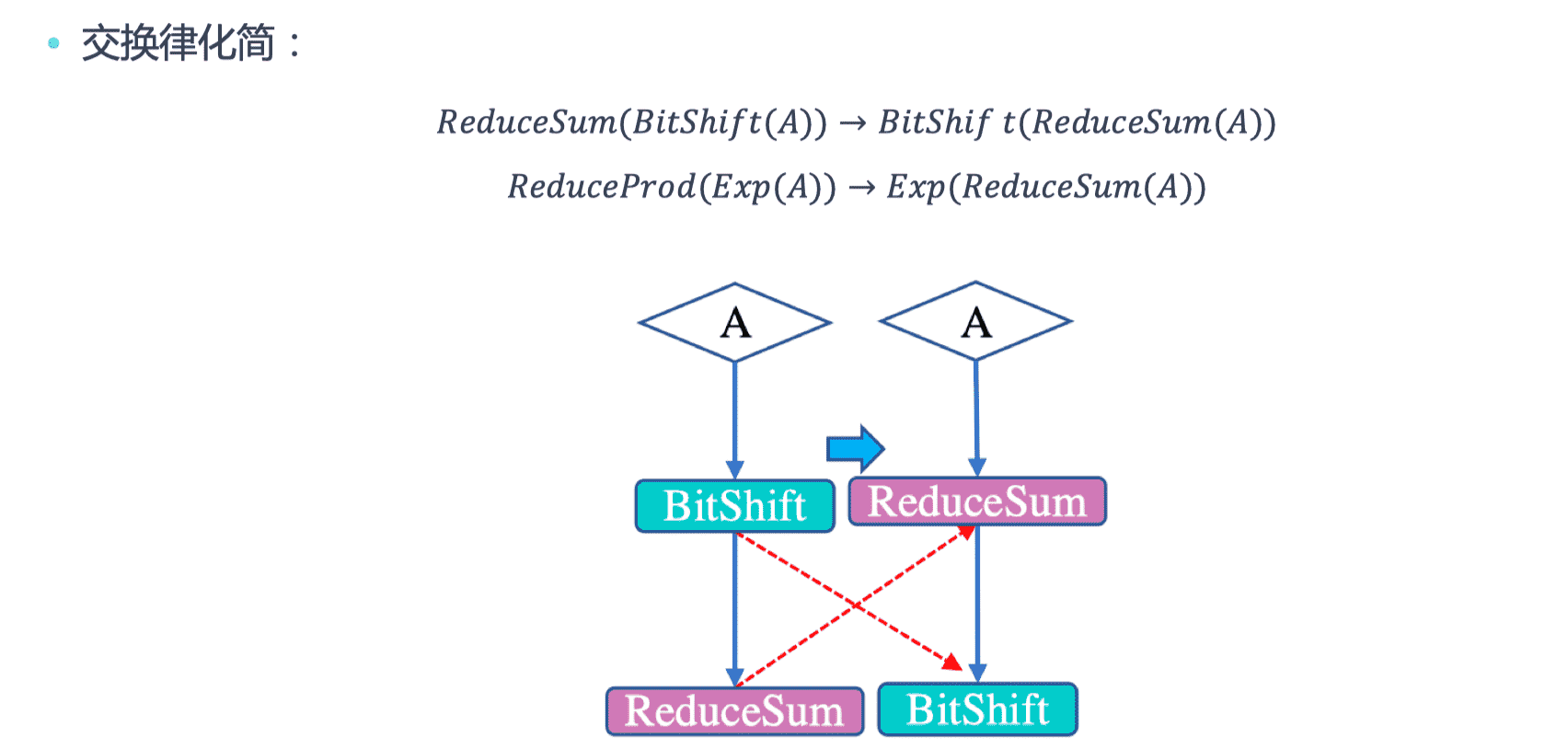
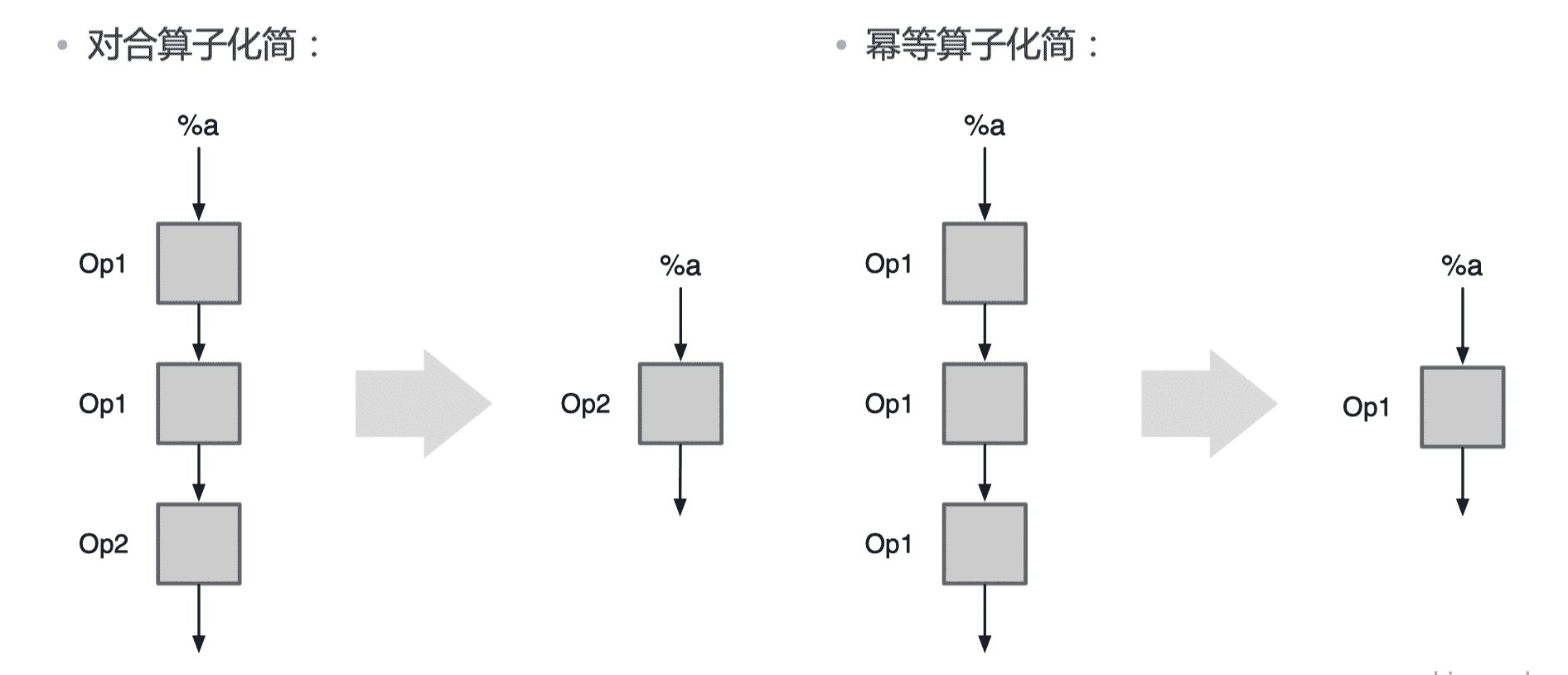
运行化简

减少运算或者执行时候，冗余的算子或者算子对。

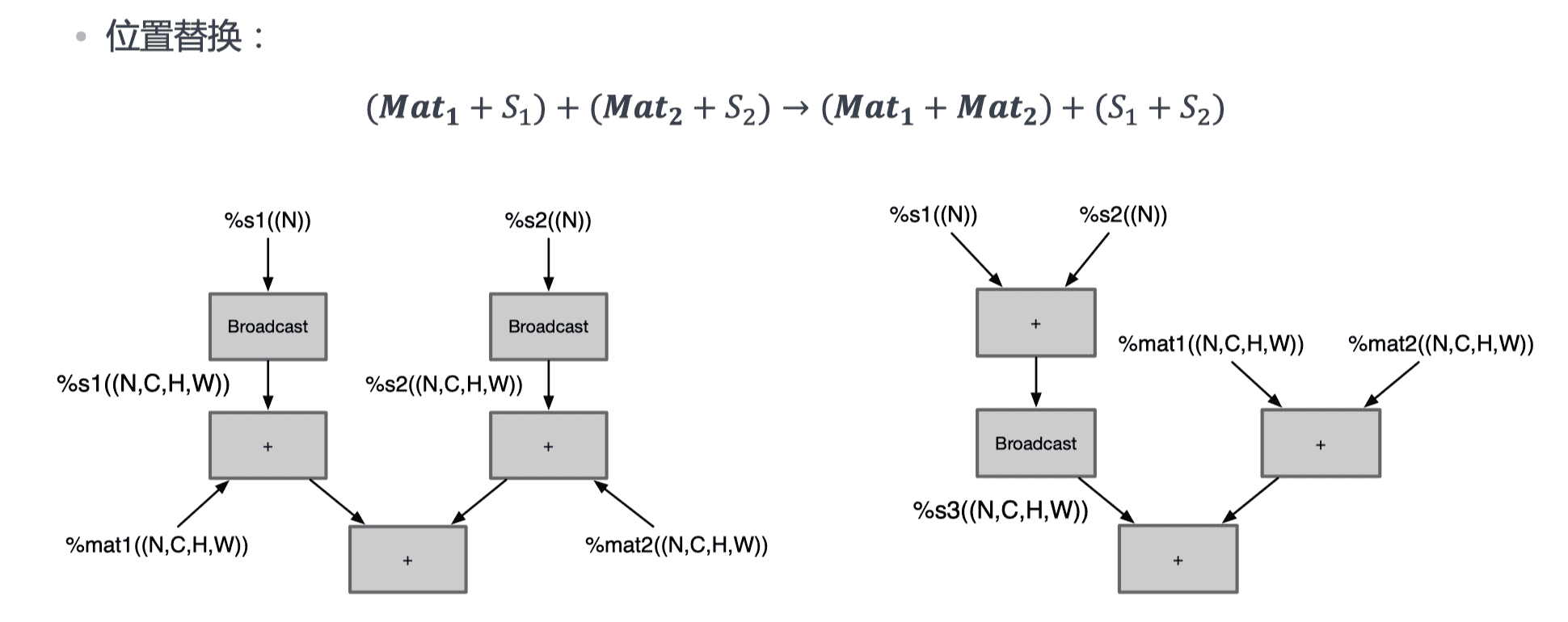
广播化简

多个张量形状 shape 不同，需要进行广播将张量的形状拓展为相同 shape 再进行运算，化简为最小计算所需的广播运算数量。

pass 的顺序（仅供参考）

  1. 神经网络相关的优化
    1. 算子融合
    2. 布局转换
    3. 内存分配
  2. 代码/计算层面的优化
    1. 常量折叠
    2. 公共子表达式消除
    3. 死代码消除
    4. 代数简化

课程笔记：AI 编译器前端优化 | 编译器

http://www.zh0ngtian.tech/posts/ee655d7b.html

作者

zhongtian

发布于

2023-01-02

更新于

2023-12-16

许可协议

评论

×