2023-12-19发表2024-03-03更新深度学习算法37 分钟读完 (大约5484个字)0次访问

从 RNN 到 Transformer | 深度学习算法

本文不涉及复杂的数学推导，仅介绍原理和流程。

RNN 与 encoder-decoder 结构

RNN

CNN 中的权重会在空间域上移动以提取特征，RNN 的权重则会在时间域上移动以提取特征。所以 CNN 一般用于处理空间域上的特征（图片等），RNN 则用于处理时间域上的特征（文本、语音等）。

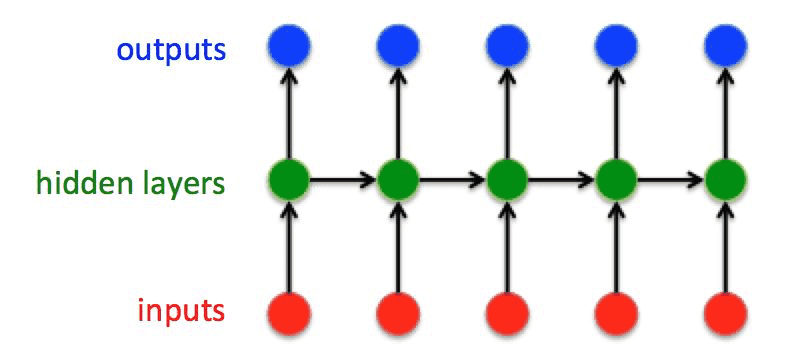
经典的 RNN 要求输⼊和输出序列必有相同的时间⻓度：

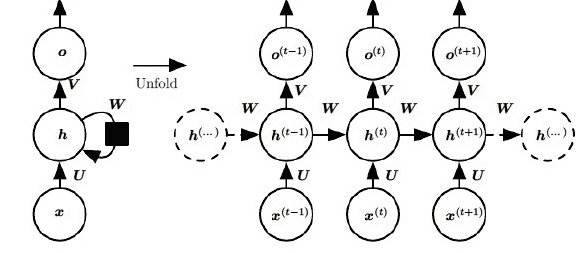
每个时刻的隐藏层状态都由当前时刻的输入和上一时刻的隐藏层决定：

$h^{(t)} = \tanh(U \cdot x^{(t)} + W \cdot h^{(t-1)})$

每个时刻的输出仅由当前时刻的隐藏层决定：

$o^{(t)} = V \cdot h^{(t)}$

RNN 可以简单的表示为：

$y_t=\mathrm{RNN}(x_t,h_{t-1})=\mathrm{RNN}(x_t,x_{t-1},\ldots,x_2,x_1)$

encoder-decoder 结构

与经典 RNN 结构不同的是，encoder-decoder 结构不再要求输⼊和输出序列有相同的时间⻓度（图中的编码器和解码器使用的仍然是 RNN）。

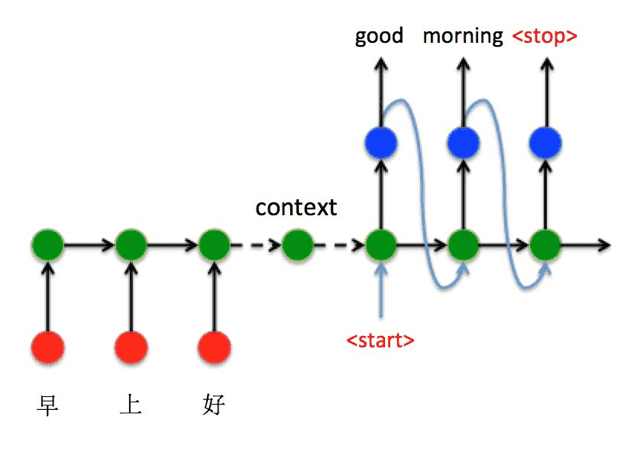
在 encoder-decoder 结构中，编码器把所有的输⼊序列都编码成⼀个统⼀的语义向量 context，然后再由解码器解码。在解码器解码的过程中，不断地将前⼀个时刻的输出作为后⼀个时刻的输⼊，循环解码，直到输出停⽌符为⽌。

embedding

上述结构所有的输入都是 token（一个词），token 可以根据字典被转换成对应的 index（一个整数），而神经网络需要的输入是向量，这就需要将 index 转换成向量。假设有 $n_c$ 个词，最简单的方法就是使用长度 $n_c$ 的 one-hot 编码，假设词库中只有「早」、「上」、「好」三个词，那么可以将这三个词编码成三个 one-hot 向量：

1
2
3

[1, 0, 0]
[0, 1, 0]
[0, 0, 1]

但是使用 one-hot 编码作为输入过于稀疏，所以使用一种更加优雅的办法：使用⼀个⼤⼩为 $[n_c,n_i]$ 的 embedding 矩阵，然后将 one-hot 编码乘以 embedding 矩阵（即获取 embedding 矩阵的第 $i_{start}=0$ ⾏），作为每个 token 对应的输⼊向量送⼊⽹络。这样，上述三个向量可能就变成了：

1
2
3

[0.34, 0.28]
[0.77, 0.02]
[0.18, 0.23]

当然，还可以使⽤ word2vec/glove/elmo/bert 等更加「精致」的嵌⼊⽅法，也可以在训练过程中迭代更新 embedding 矩阵。

注意力机制

概念

在 encoder-decoder 结构中，encoder 把所有的输入序列都编码成一个统一的语义向量 context，然后再由 decoder 解码。由于 context 包含原始序列中的所有信息，它的长度就成了限制模型性能的瓶颈。如机器翻译问题，当要翻译的句子较长时，一个 context 可能存不下那么多信息，就会造成精度的下降。除此之外，如果按照上述方式实现，只用到了编码器的最后一个隐藏层状态，信息利用率低下。所以一个很好的解决方法是利用 encoder 所有隐藏层状态解决 context 长度限制问题。

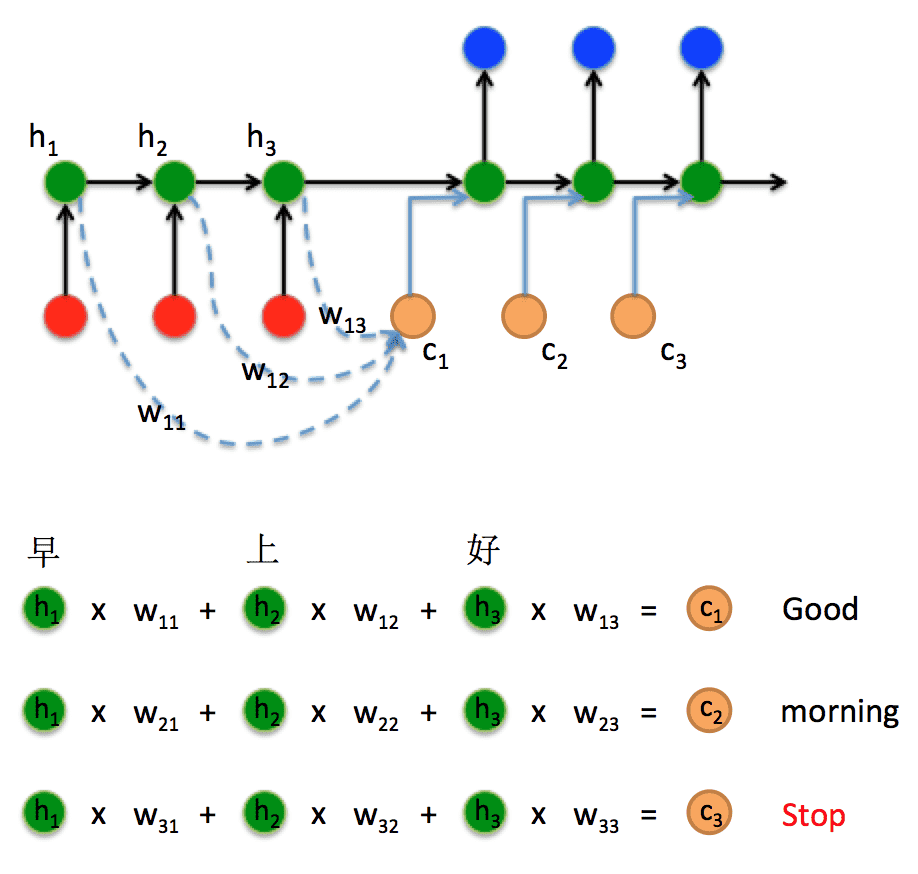
然后将 c1 向量与前一个状态 h3 拼接在一起形成一个新的向量输入到隐藏层计算结果。decoder 时刻 t=2 和 t=3 同理，就可以解决 context 长度限制问题。由于 w11, w12, w13 不同，就形成了一种对编码器不同输入对应的「注意力」机制（权重越大注意力越强）。

注意力模型计算的是输入序列与额外的上下文之间的联系，自注意力模型计算的是输入序列内不同位置之间的关联性。以句子「He went to the bank and learned of his empty account, after which he went to a river bank and cried.」为例，句子中有两个「bank」，但是其代表的意义是完全不同的。在这里模型可以根据「his empty account」来推断第一个「bank」为银行，根据「river」可以推断第二个「bank」为岸边。而自注意力指代的就是通过计算输入序列内不同位置之间的关联性得到权重，然后将这些权重应用于输入序列的每个位置，以获取位置自适应的表示。

Luong attention

Luong attention 是一种全局注意力模型，其思想是在推导 context 的时候考虑编码器的所有隐藏状态，在全局注意力模型中，通过将某个解码器隐藏状态与每个编码器隐藏状态进行结合，得出大小等于编码器时间步数的向量。

为了进一步减少计算代价，在解码过程的每一个时间步仅关注输入序列的一个子集，于是在计算每个位置的 attetnion 时会固定一个上下文窗口，而不是在全局范围计算 attention，这就是局部注意力模型。局部注意力只会关注部分隐状态。

下面以 Luong attention 为例介绍 attention 的具体计算流程（摘自《完全解析RNN, Seq2Seq, Attention注意力机制》）：

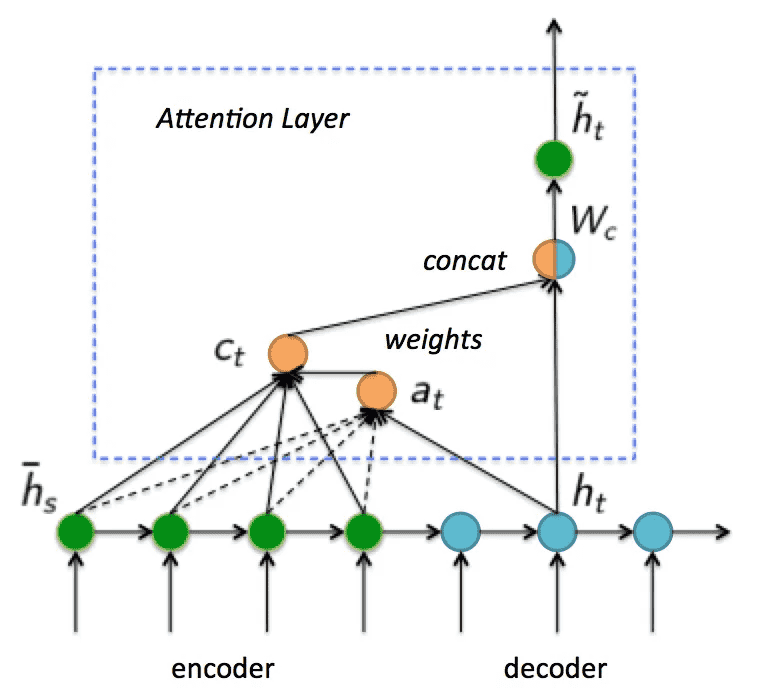
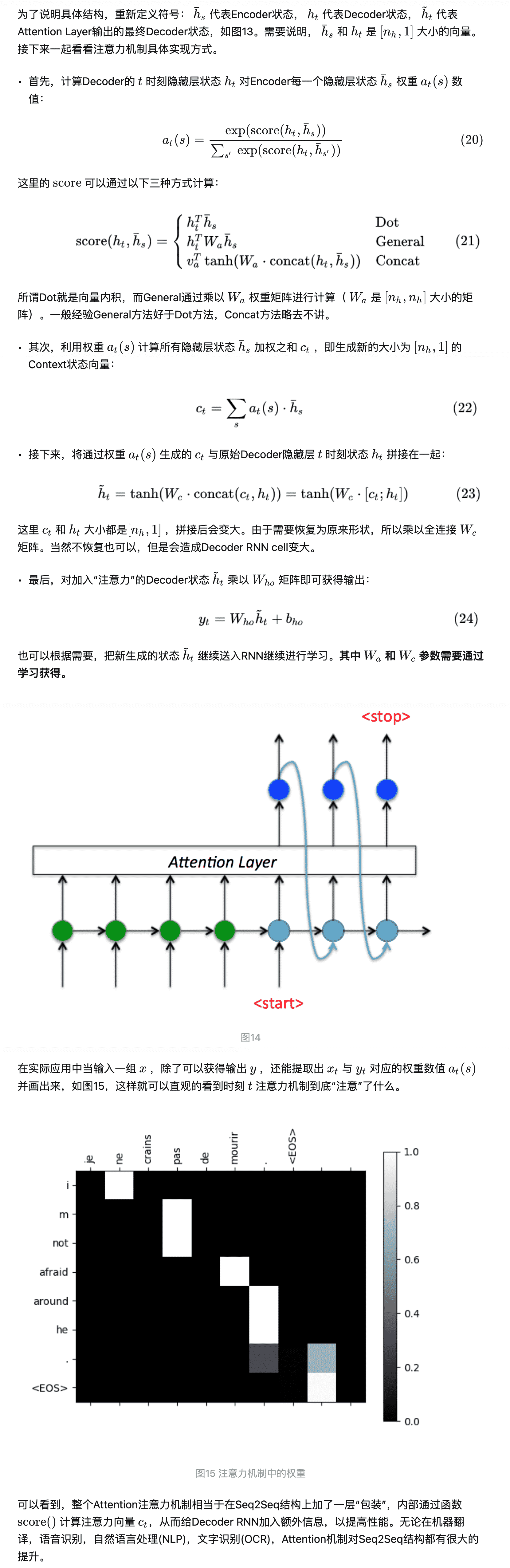
attention 机制的本质

我们可以这样来看待 attention 机制：将 source 中的构成元素想象成是由一系列的 key-value 数据对构成，此时给定 target 中的某个元素 query，通过计算 query 和各个 key 的相似性或者相关性，得到每个 key 对应 value 的权重系数，然后对 value 进行加权求和，即得到了最终的 attention 数值。所以本质上 attention 机制是对 source 中元素的 value 值进行加权求和，而 query 和 key 用来计算对应 value 的权重系数。

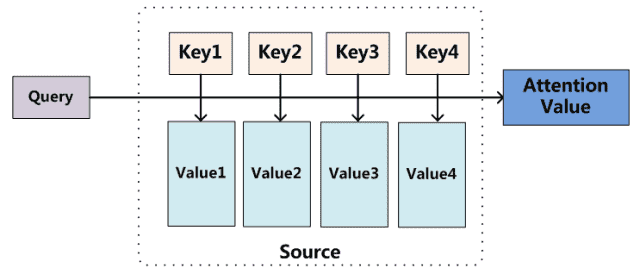
也可以将 attention 机制看作一种软寻址：source 可以看作存储器内存储的内容，元素由地址 key 和值 value 组成，当前有个 key=query 的查询，目的是取出存储器中对应的 value 值，即 attention 数值。通过 query 和存储器内元素 key 的地址进行相似性比较来寻址，之所以说是软寻址，指的不像一般寻址只从存储内容里面找出一条内容，而是可能从每个 key 地址都会取出内容，取出内容的重要性根据 query 和 key 的相似性来决定，之后对 value 进行加权求和，这样就可以取出最终的 value 值，也即 attention 值。

那么怎么理解 attention 模型的物理含义呢？比如对于机器翻译来说，本质上 attention 模型是输出 target 句子中某个单词和输入 source 句子每个单词的对齐模型。

self-attention 与 cross-attention

根据 query 和 key-value 来源不同，常用的 attention 机制包括 self-attention 和 cross-attention。

在 self-attention 中，输入序列被分成三个向量（即查询向量、键向量和值向量），这三个向量均是来自于同一组输入序列，用于计算每个输入元素之间的注意力分数。因此，self-attention 可以用于在单个序列中学习元素之间的依赖关系，例如用于语言建模中的上下文理解。

在 cross-attention 中，有两个不同的输入序列，其中一个序列被用作查询向量，另一个序列被用作键和值向量。cross-attention 计算的是第一个序列中每个元素与第二个序列中所有元素之间的注意力分数，通过这种方式来学习两个序列之间的关系。例如，在图像字幕生成任务中，注意力机制可以用来将图像的特征与自然语言描述的句子相关联。

self-attention 的计算流程

1. 从编码器的每个输⼊向量中创建三个向量

因此，对于每个单词，我们创建⼀个 query 向量、⼀个 key 向量和⼀个 value 向量。这些向量是通过将 embedding 向量与三个训练后的矩阵相乘得到的：$X_ 1$ 与权重矩阵 $W^Q$ 相乘得到相应的 query 向量 $q_1$, 同样可以得到输⼊序列中每个单词对应的 $k_1$ 和 $v_1$。这些新向量的维度比 embedding 向量小。它们的维数是 64，而 embedding 向量和编码器输入/输出向量的维数是 512。

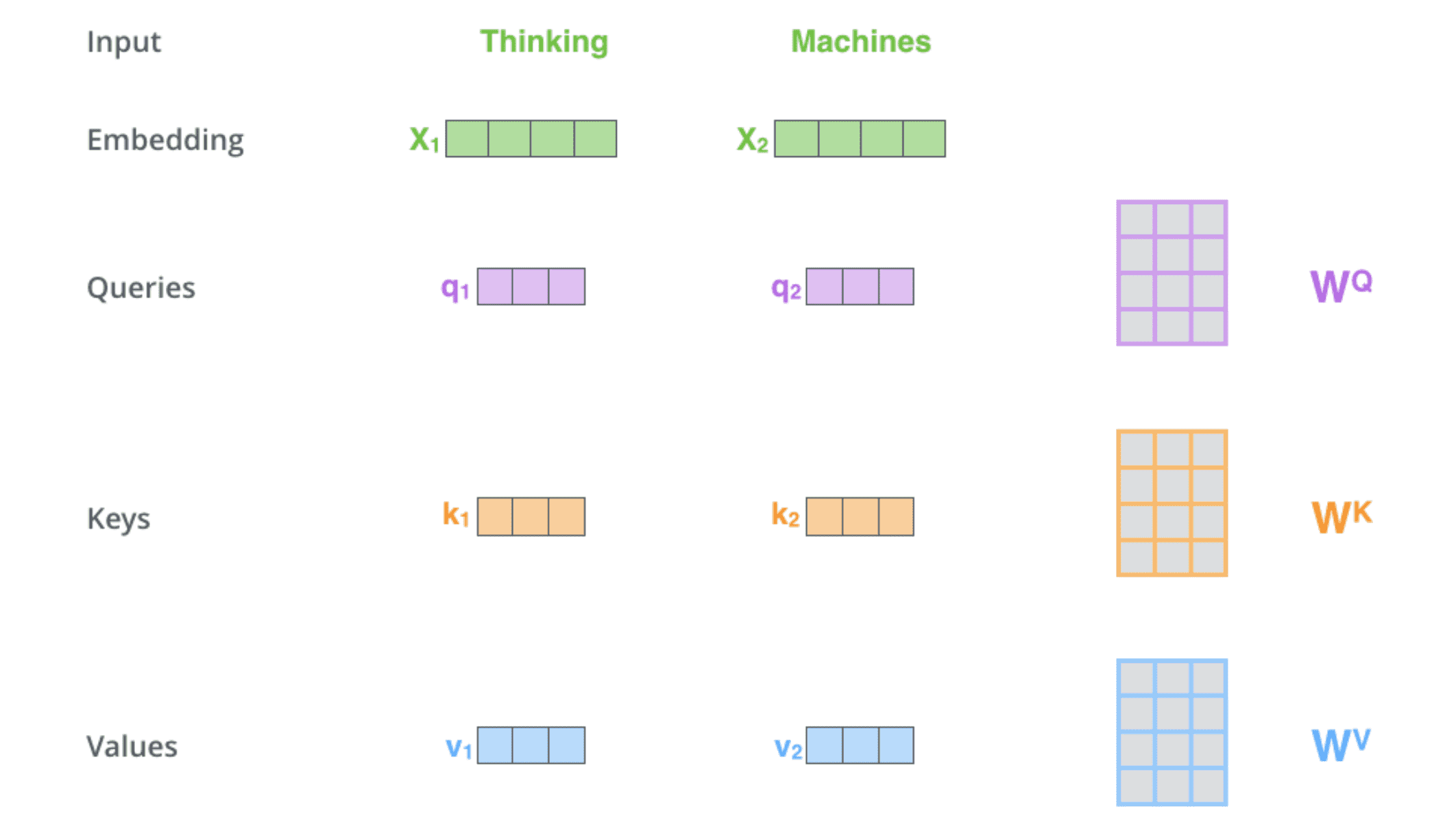
2. 计算注意⼒得分

假设我们要计算本例中第⼀个单词的⾃注意⼒得分，这需要对输⼊句⼦中的每个单词进⾏打分，这个分数决定了在编码第⼀个单词时，对其他单词的关注程度。这个得分是通过计算 query 向量与各个单词的 key 向量的点积得到的（正如前面提到的软寻址模型，这里需要计算 query 和 key 的相似度）。

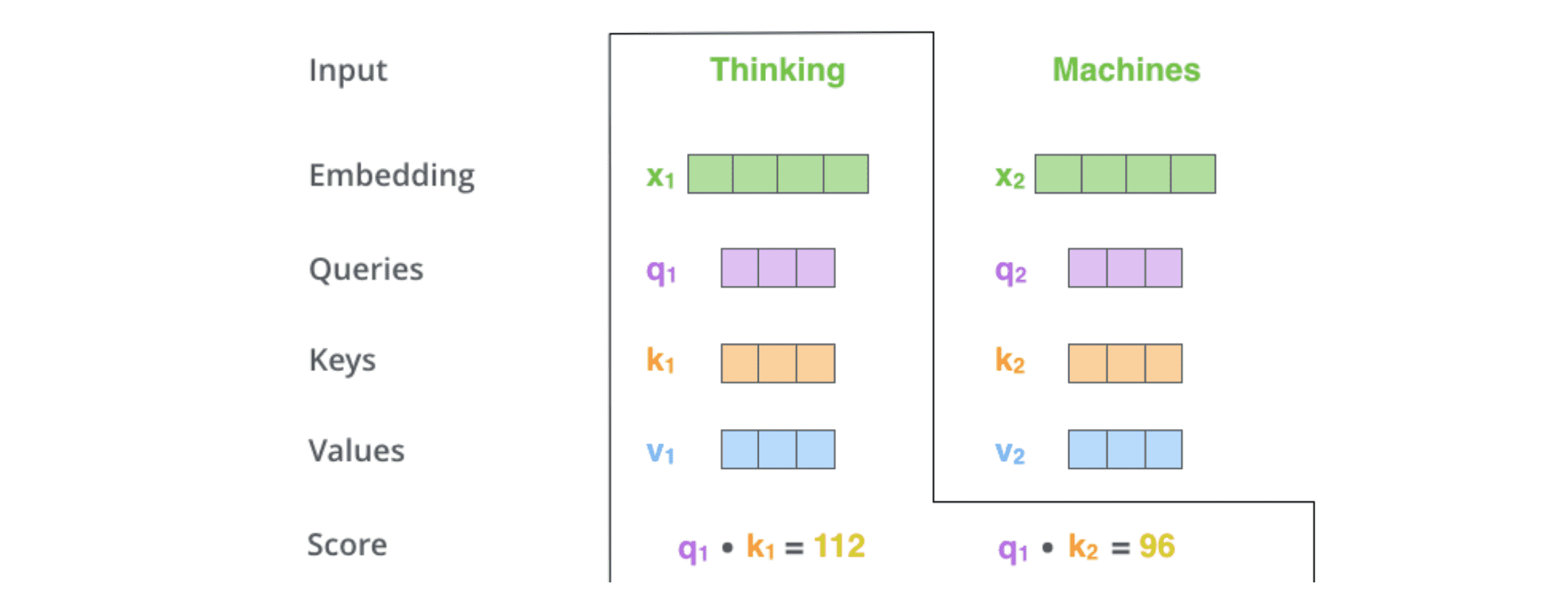
3. 对 self-Attention socre 进行缩放和归一化，得到 softmax 分数

对第二步中的分数除以 8（默认为 key 向量的维数 64 的平⽅根，这能让梯度更新的过程更加稳定），然后将结果进⾏ softmax 操作。

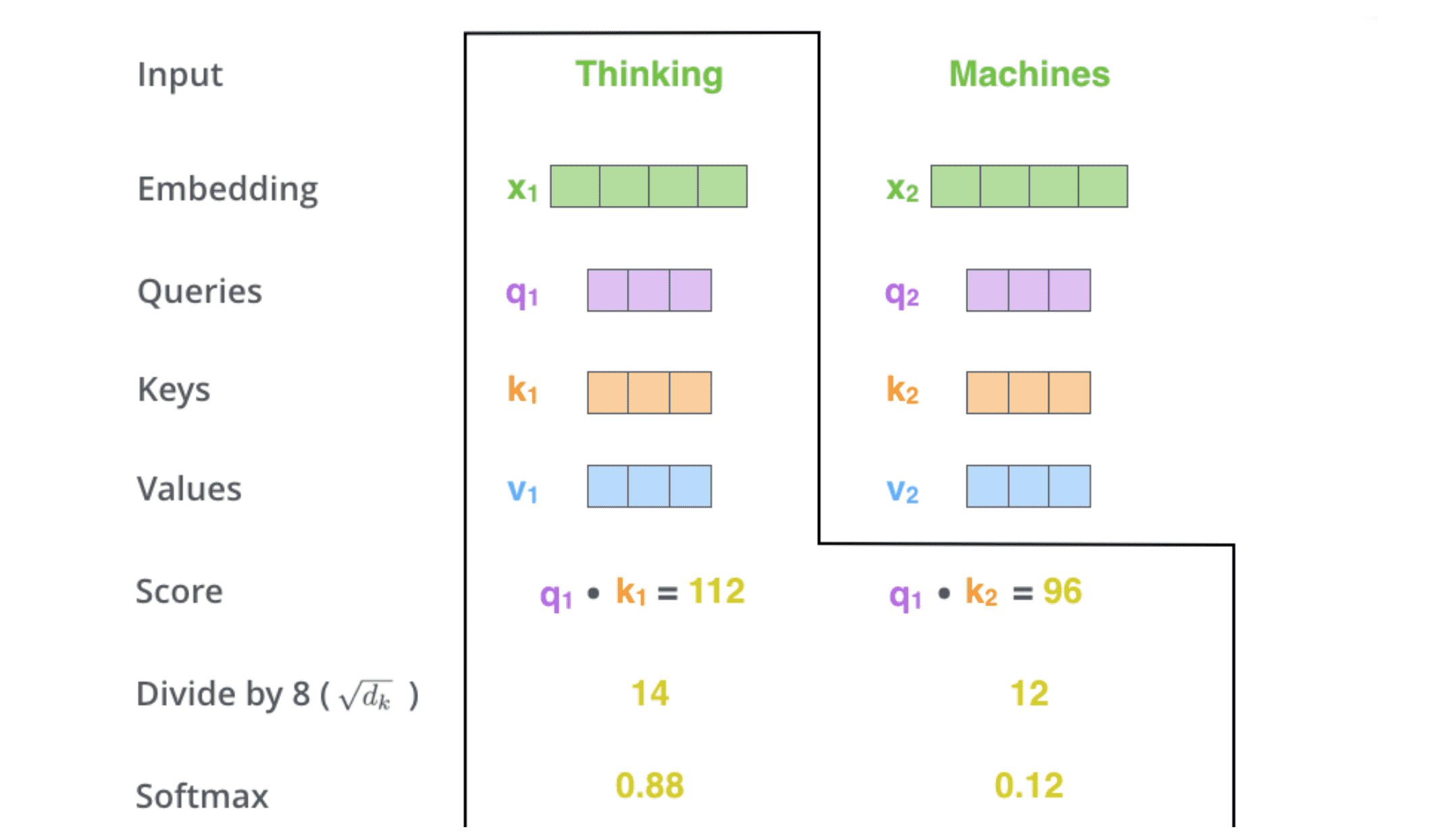
该分数的结果决定了每个单词在第一个位置上的相关程度。显然，这个单词本身的位置会有最⾼的分数。

4. 将 softmax socre 乘以 value 向量，求和得到 attention value

每个 value 向量乘以 softmax 分数得到加权的 v1 和 v2，对加权的 v1 和 v2 进行求和得到 z1。这样就计算出了第一个词的 attention value。其他的词用相同的方法进行计算。加权的思想是尽量保持想要关注的单词的 value 值不变，⽽掩盖掉那些不相关的单词（将它们乘以一个较小的系数）。

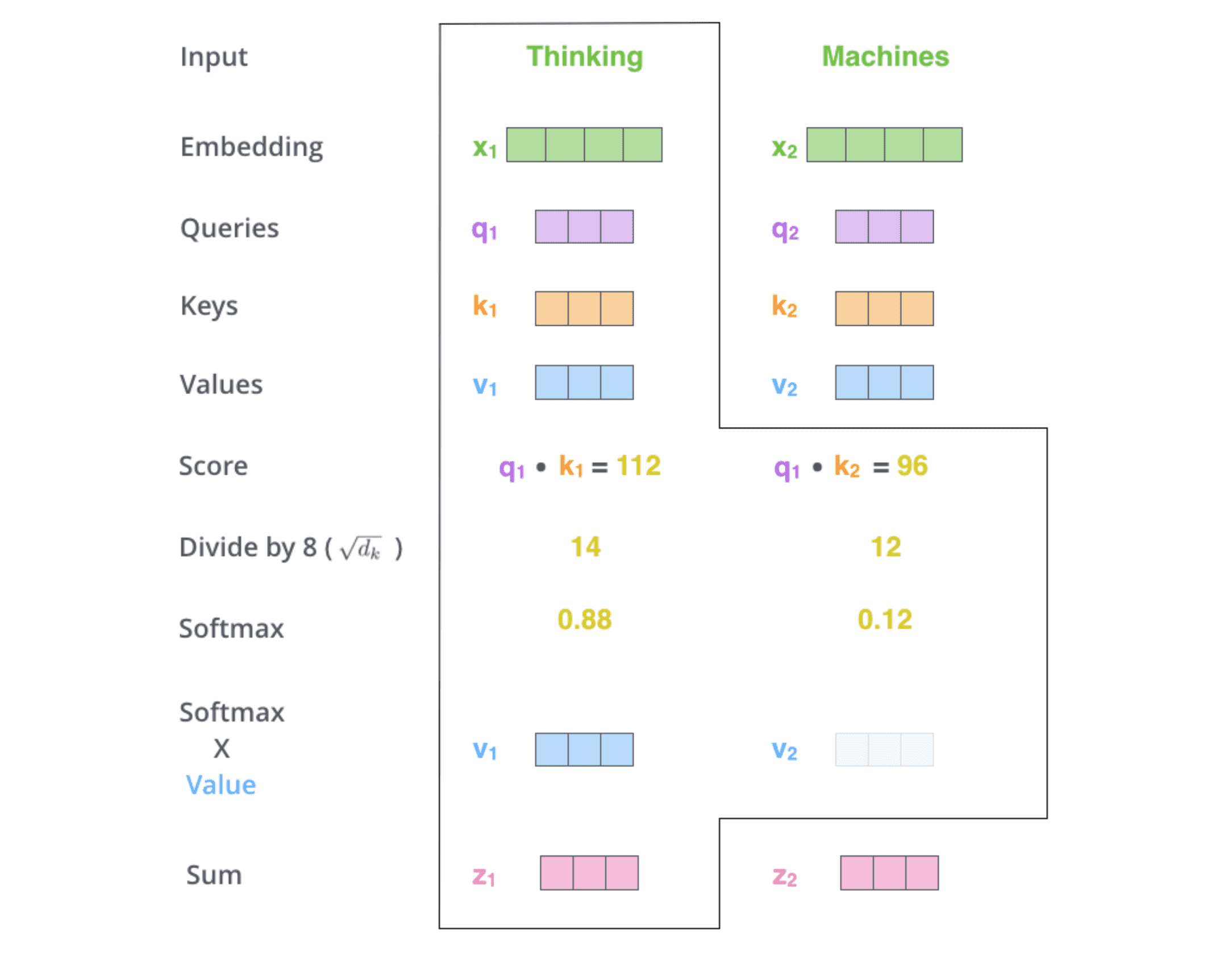
这就是 self-attention 的计算流程。下面使用动图展示下整个过程：

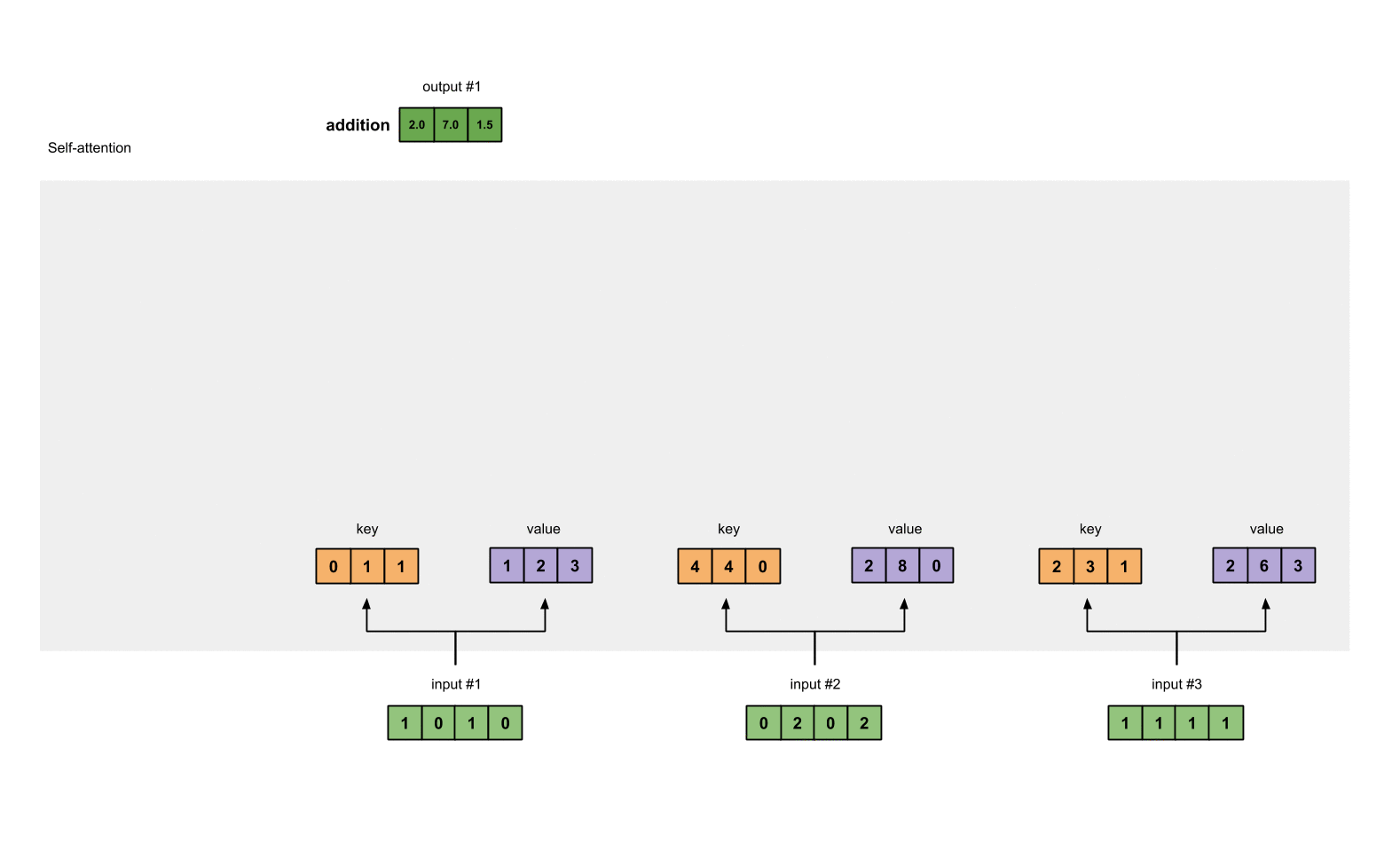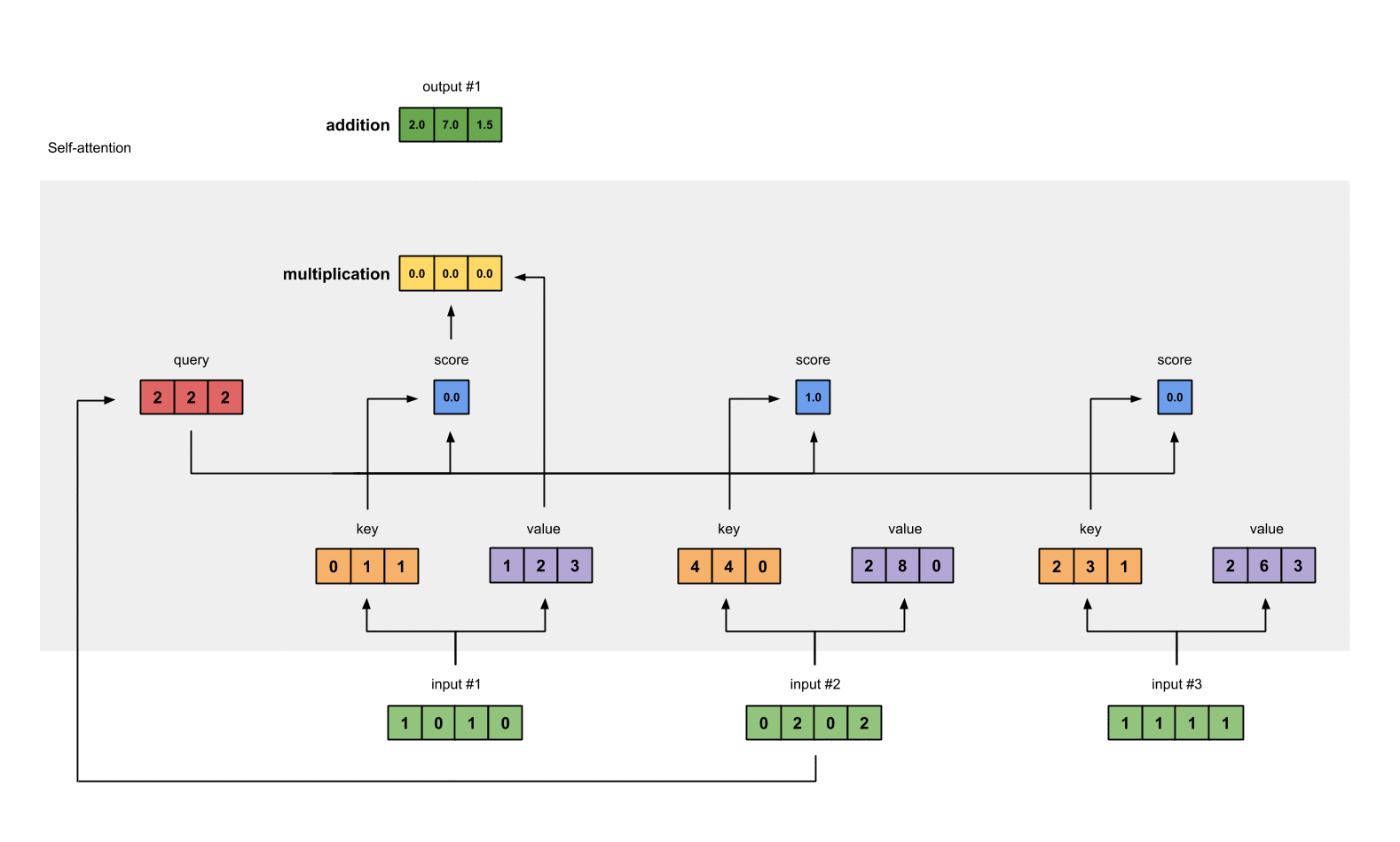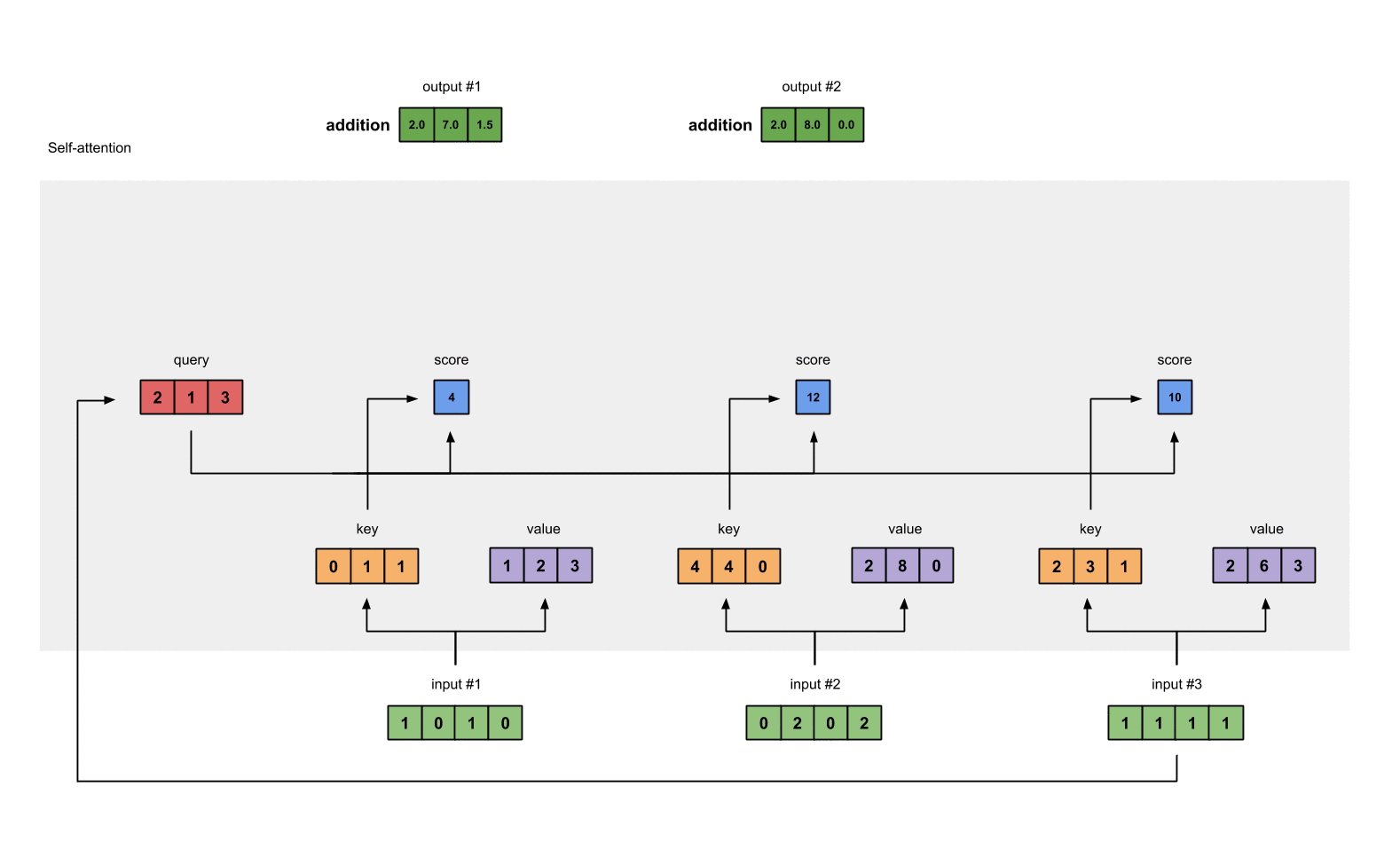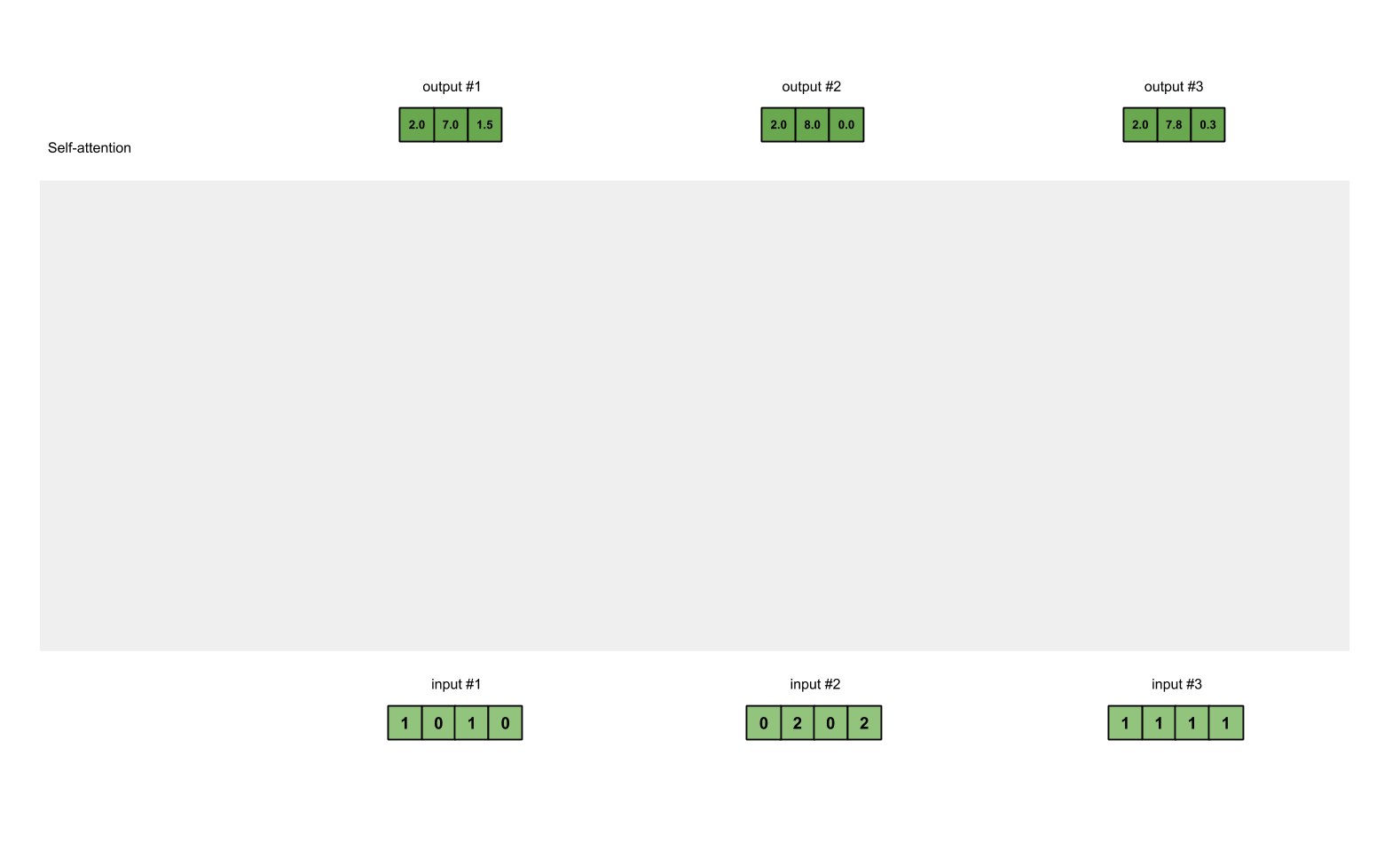
在实际的实现中，为了更快的处理，这种计算是以矩阵形式进⾏的。

self-attention 计算的矩阵形式

把多个 embedding 向量组成的矩阵 X 乘以训练得到的的权重矩阵（$W^Q$, $W^K$, $W^V$）。X 矩阵中的每一行对应于输入句子中的一个单词。图中可以再次看到 embedding 向量（512 维，即图中的 4 个方格长度）和 query/key/value 向量（64 维，即图中的 3 个方格长度）大小的差异。

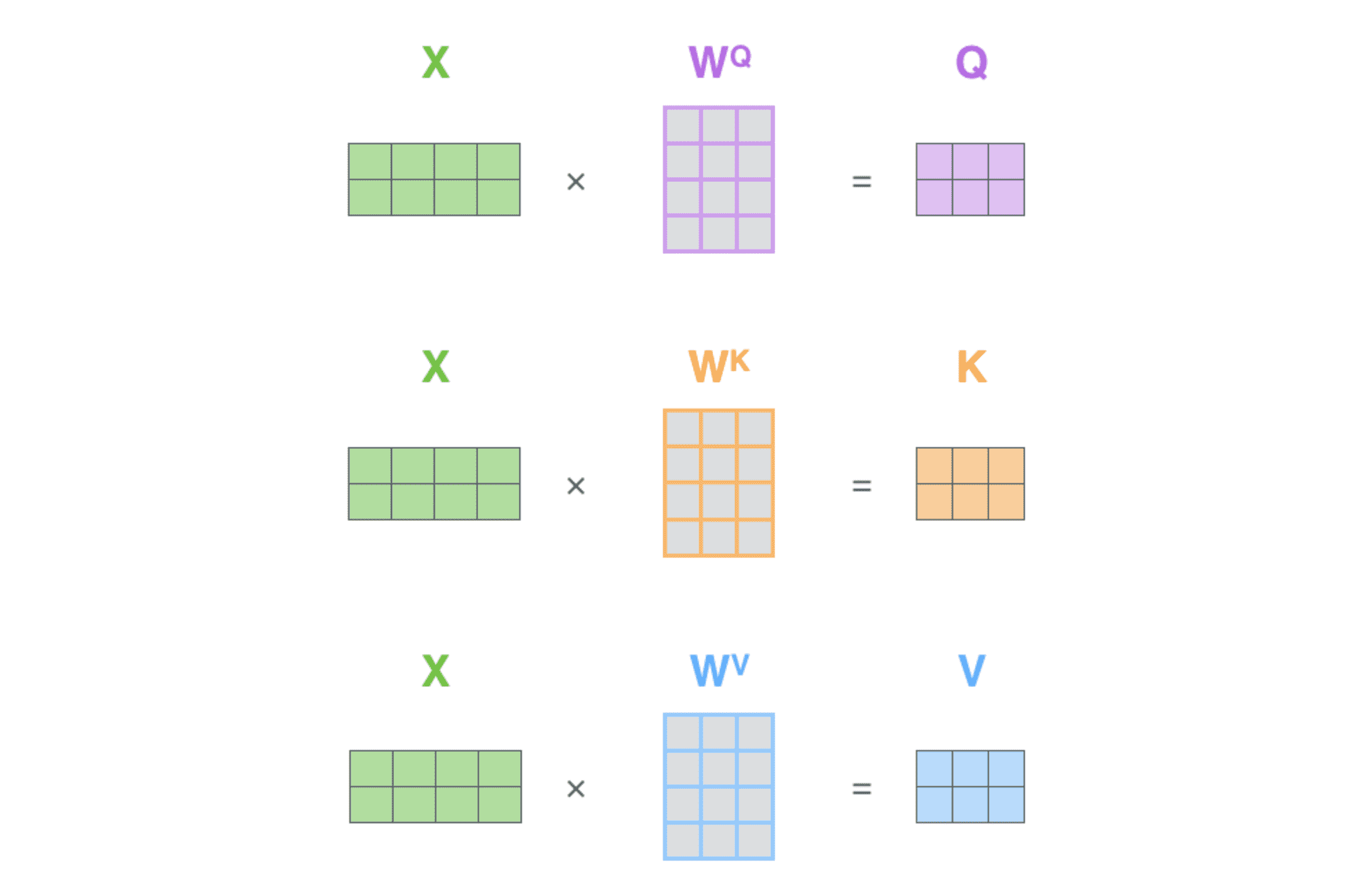
由于处理的是矩阵，可以将上一节中的的第 2、3、4 步合并为⼀个公式：

multi-head attention

多头⾃注意力给了⾃注意⼒层多个「表示⼦空间」。正如下图所示，多头⾃注意⼒有不⽌⼀组 query/key/value 权重矩阵，⽽是有多组（Transformer 使⽤ 8 个「头」）。每⼀个都是随机初始化的，然后经过训练，每个权重矩阵被⽤来将输⼊向量投射到不同的表示⼦空间。

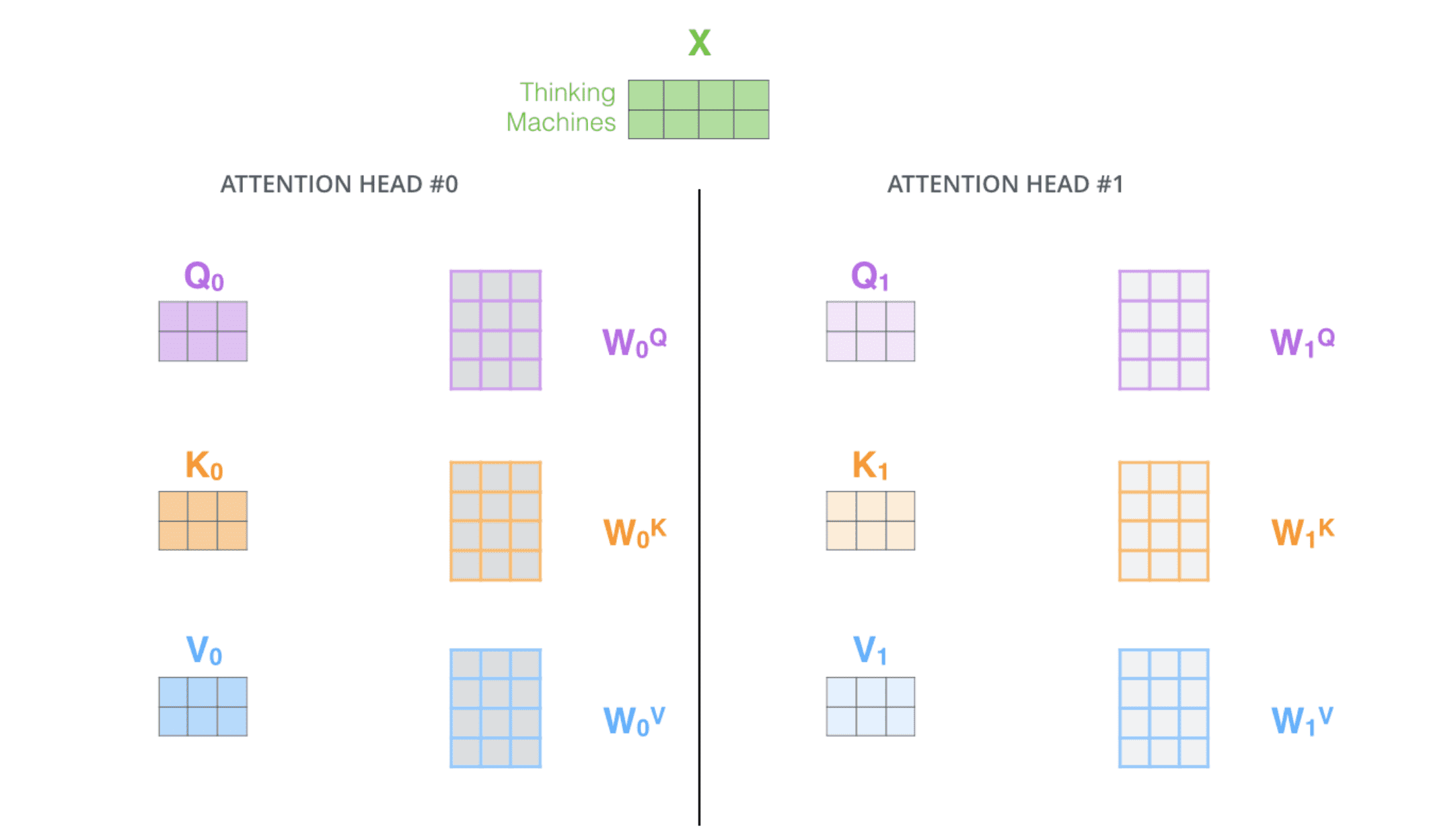
⽤不同的权重矩阵做 8 次不同的计算，我们最终得到 8 个不同的 Z 矩阵。在 Transformer 中，注意力层的后面是前馈层，前馈层只需要⼀个矩阵（每个单词对应⼀个）。所以需要把这 8 个矩阵压缩成⼀个矩阵：把这些矩阵拼接起来然后⽤⼀个额外的权重矩阵与之相乘。

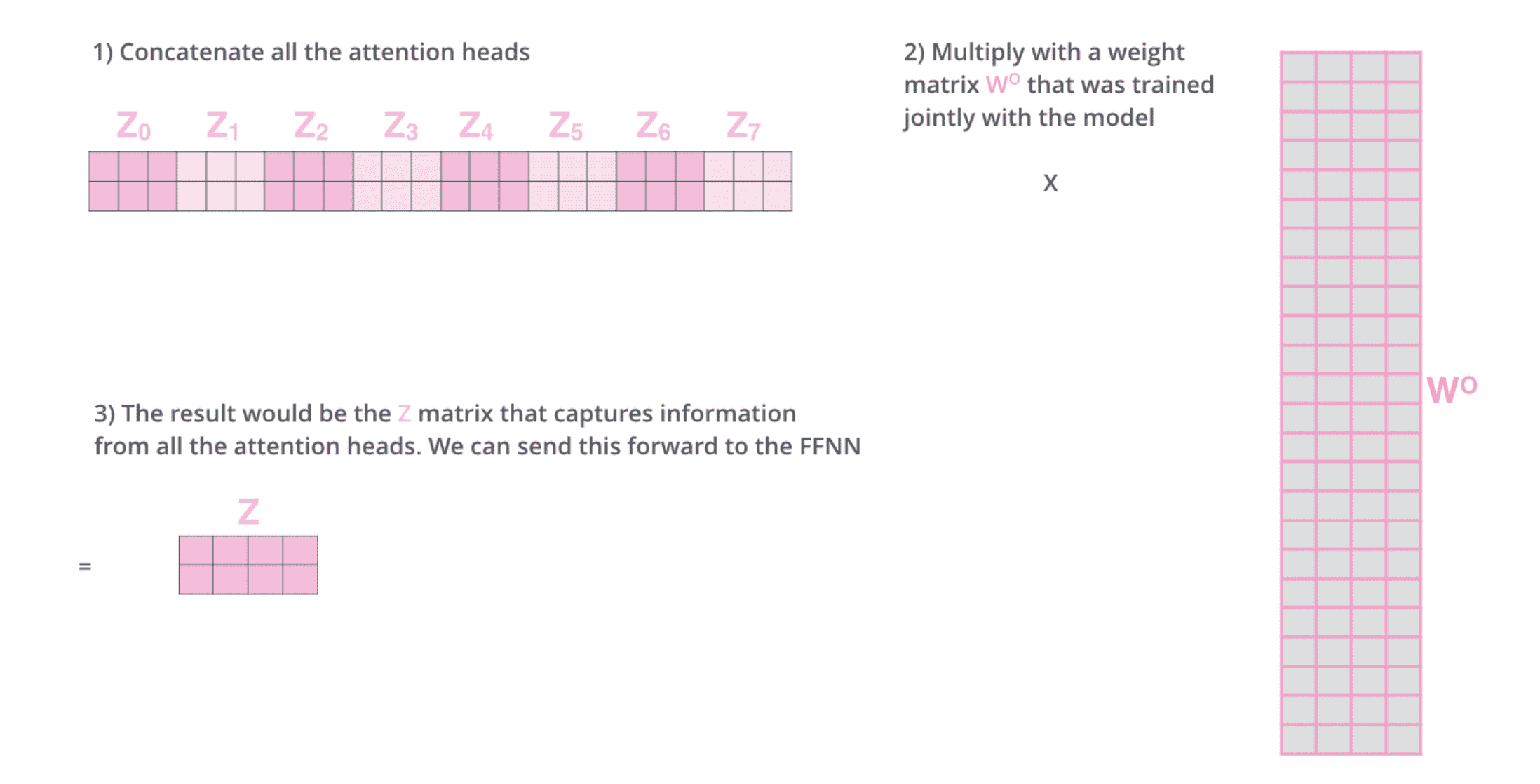
这就是多头⾃注意⼒的全部内容，将整个计算过程放在⼀张图上看看：

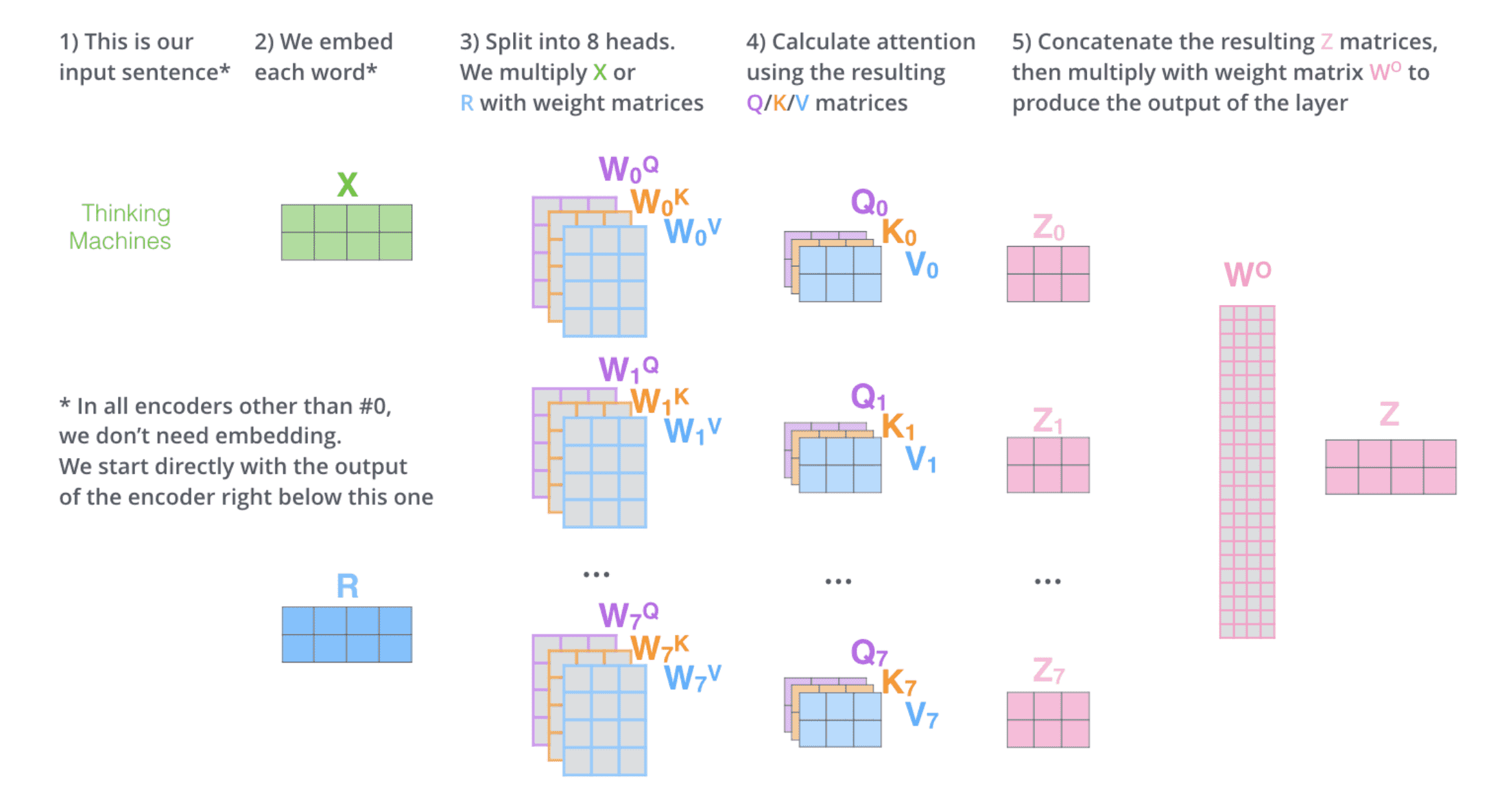
masked self-attention (causal self-attention)

掩码自注意力机制确保序列中某个位置的输出仅基于先前位置的已知输出，而不基于未来位置。简而言之，它确保了每个下一词的预测仅取决于前面的词。

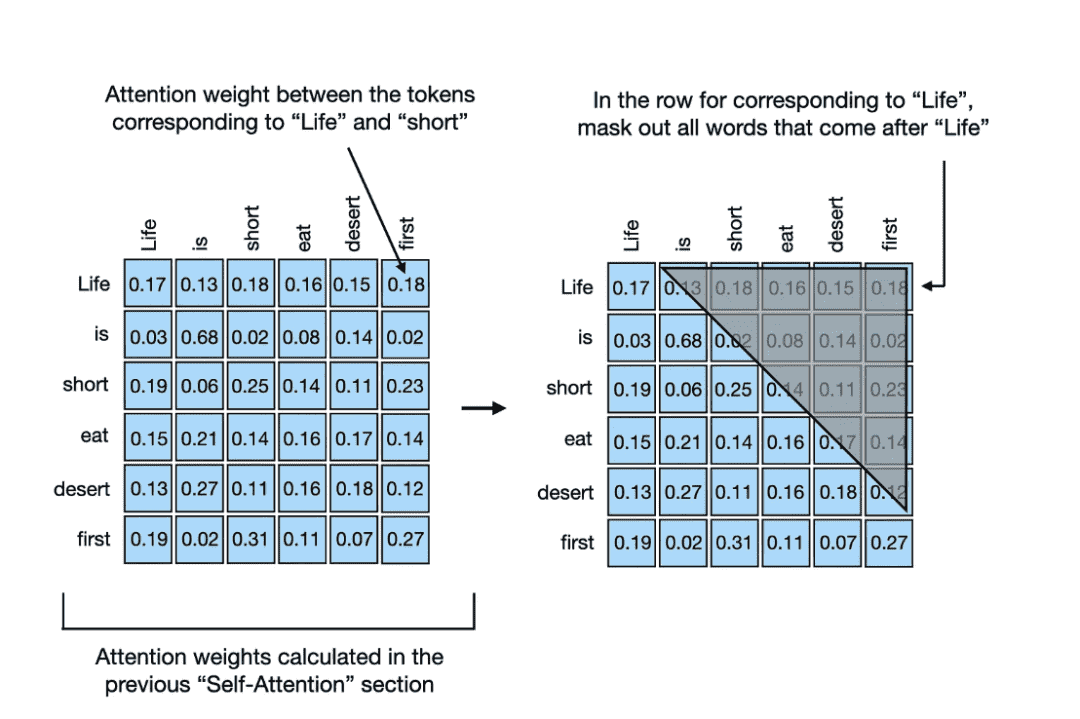
在将掩码对应的注意力权重置零以后，每行中的注意力权重的总和不再为 1。为解决这一问题，可以归一化这些行，使它们的总和再次为 1。在神经网络中，像 Transformer 模型一样对注意力权重进行归一化，有两个主要优点：首先，总和为 1 的归一化注意力权重类似于概率分布，有助于按比例解释模型对输入的不同部分的注意力；其次，将注意力权重总和限制为 1，有助于控制权重和梯度的规模，改善训练的动态性。

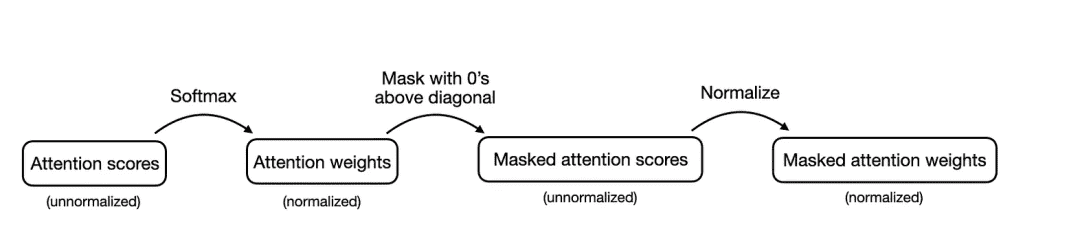
在上述掩码自注意力过程中，首先计算注意力得分，然后计算注意力权重，掩码处理对角线以上的注意力权重，最后重新归一化注意力权重：

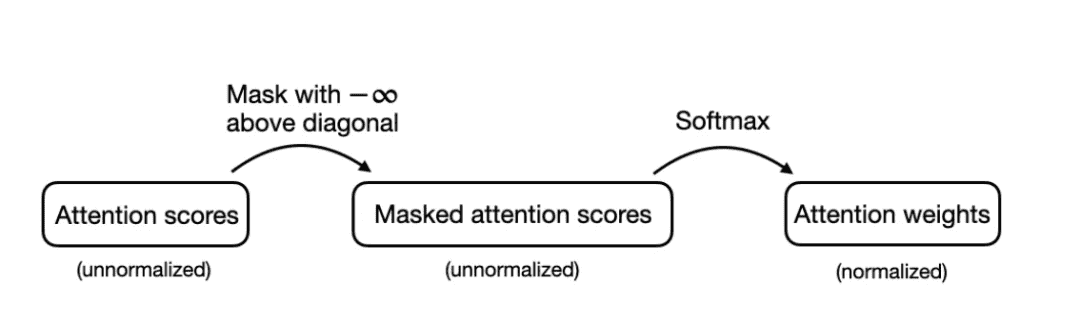
有一种更有效的方法可以达到相同结果。在这种方法中，在得到注意力得分后，并在将值输入 softmax 函数以计算注意力权重前，将对角线以上的值替换为负无穷：

Transformer

整体结构

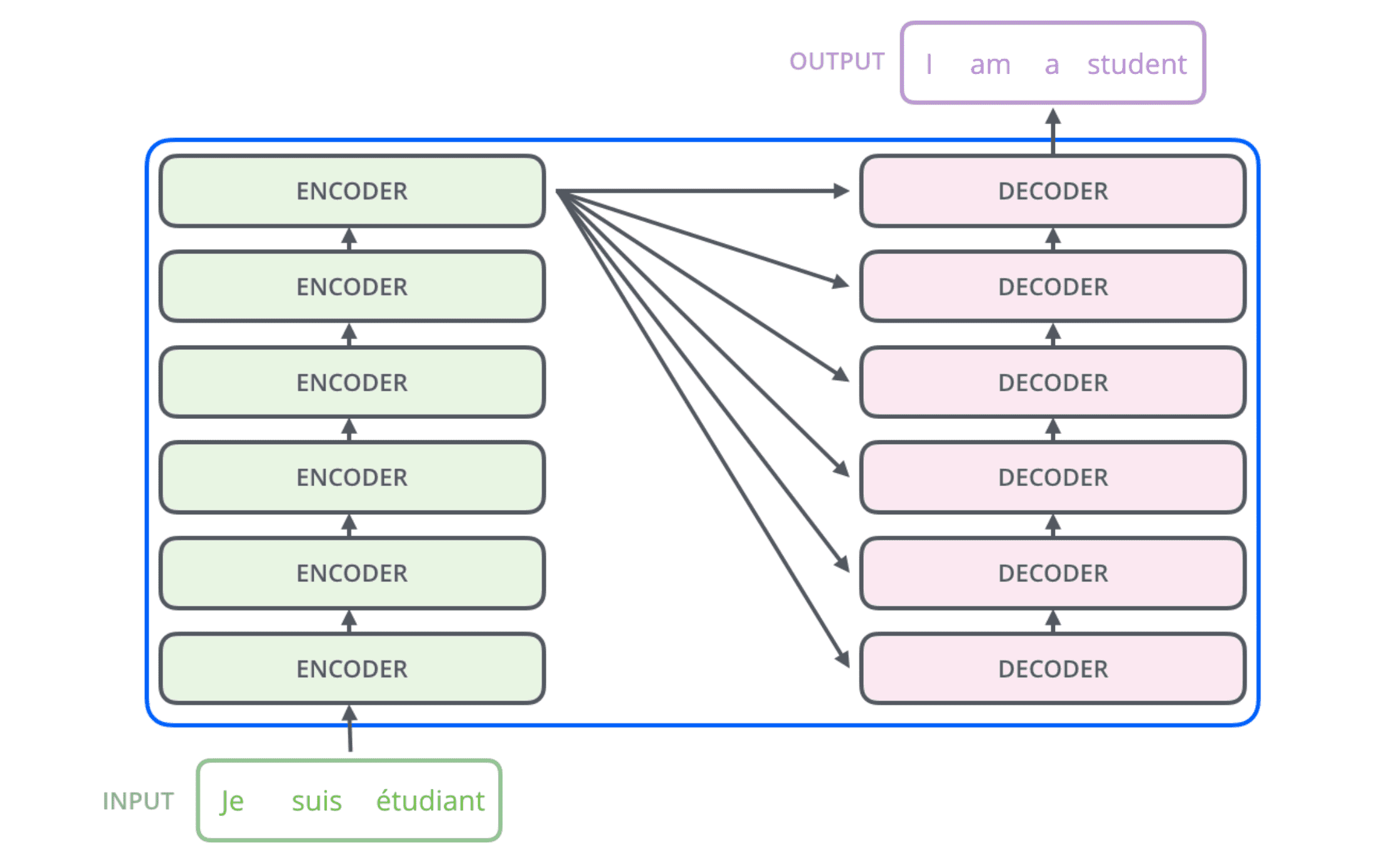
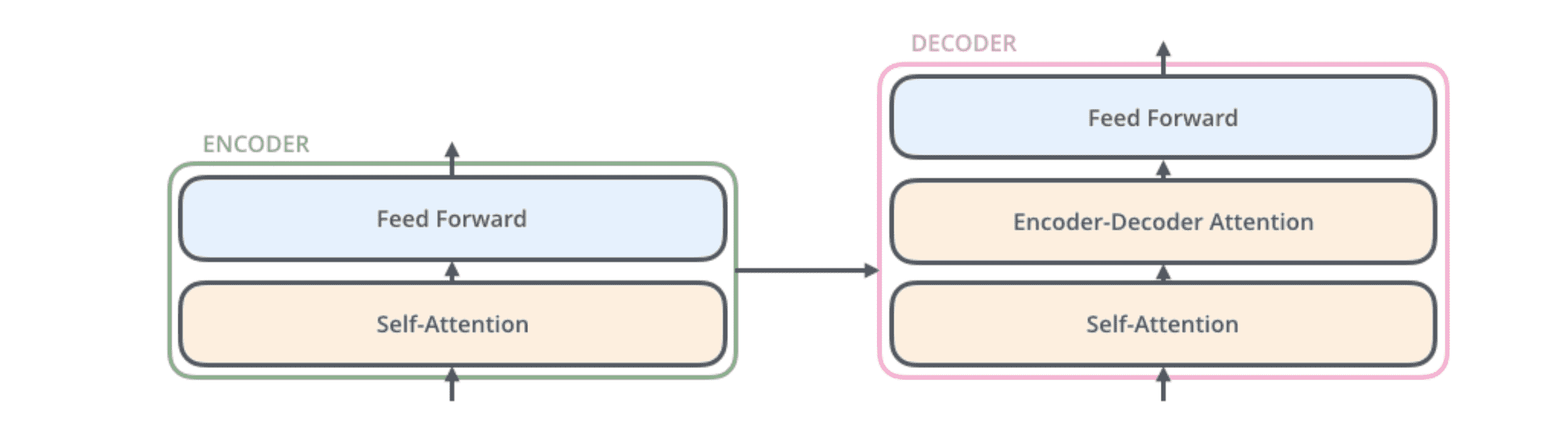
解码器相比编码器多了一个编码器-解码器注意⼒层，它是一个交叉注意力层：从前⾯的⽹络层创建 query 矩阵，从编码器的输出中创建 key 矩阵和 value 矩阵。

如果仅考虑⼀个由 2 个编码器和 2 个解码器组成的 Transformer，它看起来是这样的：

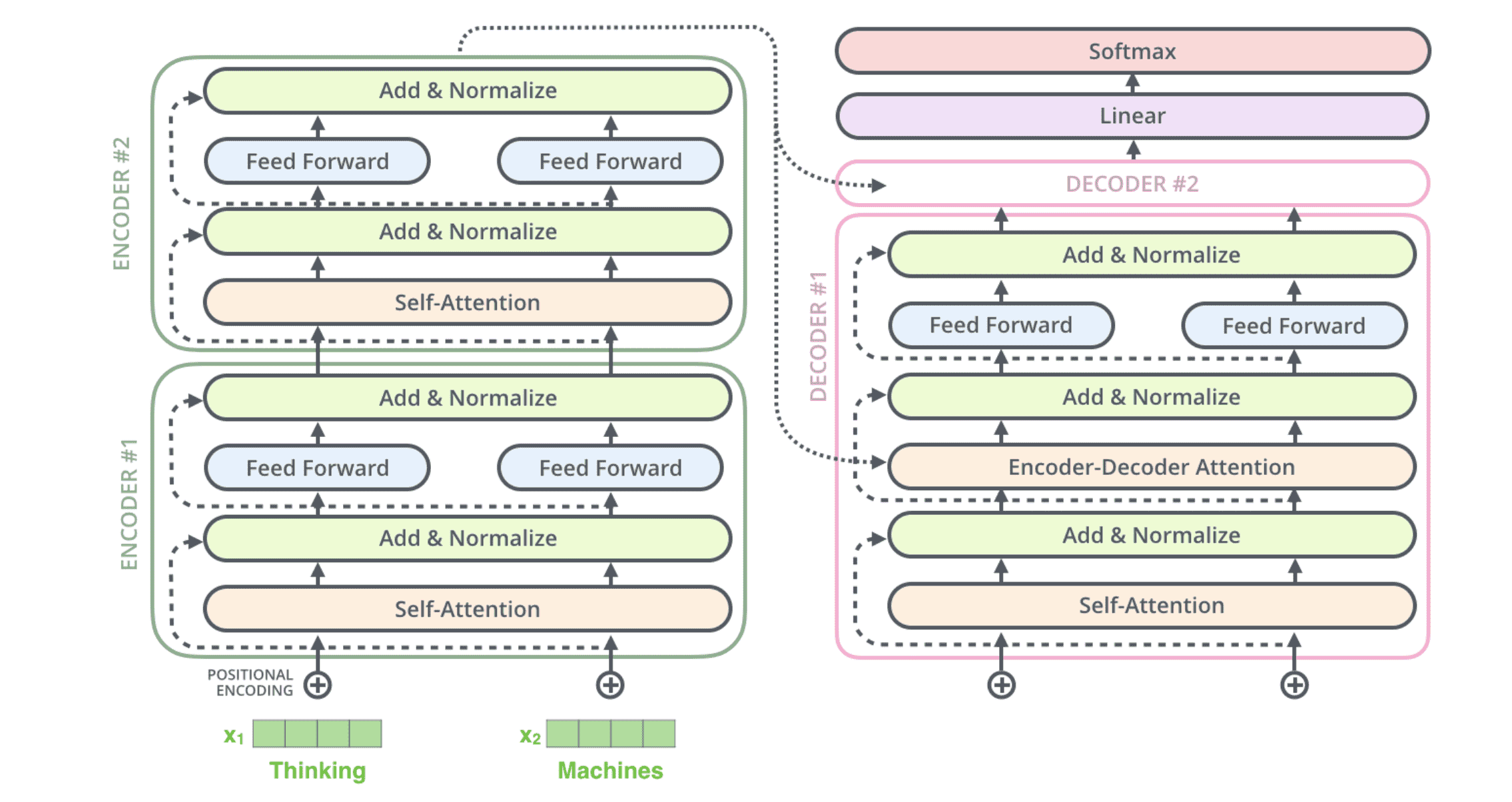
可以和原论文中的图对比着看：

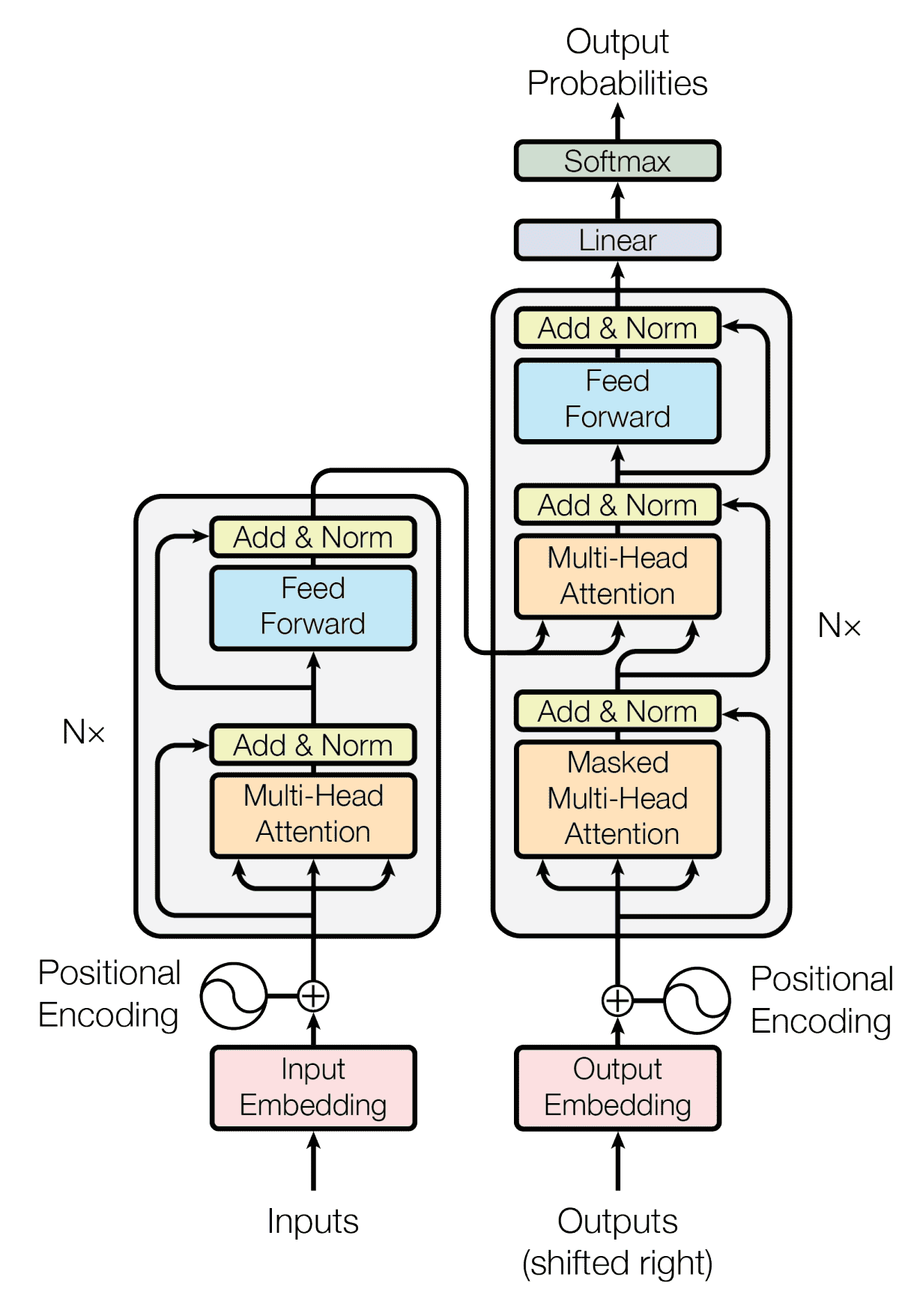
编码器

⾸先使⽤ embedding 算法将每个输⼊单词转换为⼀个向量。

所有编码器都会以⼀个向量列表为输⼊（每个向量有 512 维），最底部的编码器接收的是 embedding 向量，但其他编码器中接收的是在其前面的编码器的输出。这个列表的⼤⼩是超参数，基本上是训练数据集中最⻓的句⼦的⻓度。

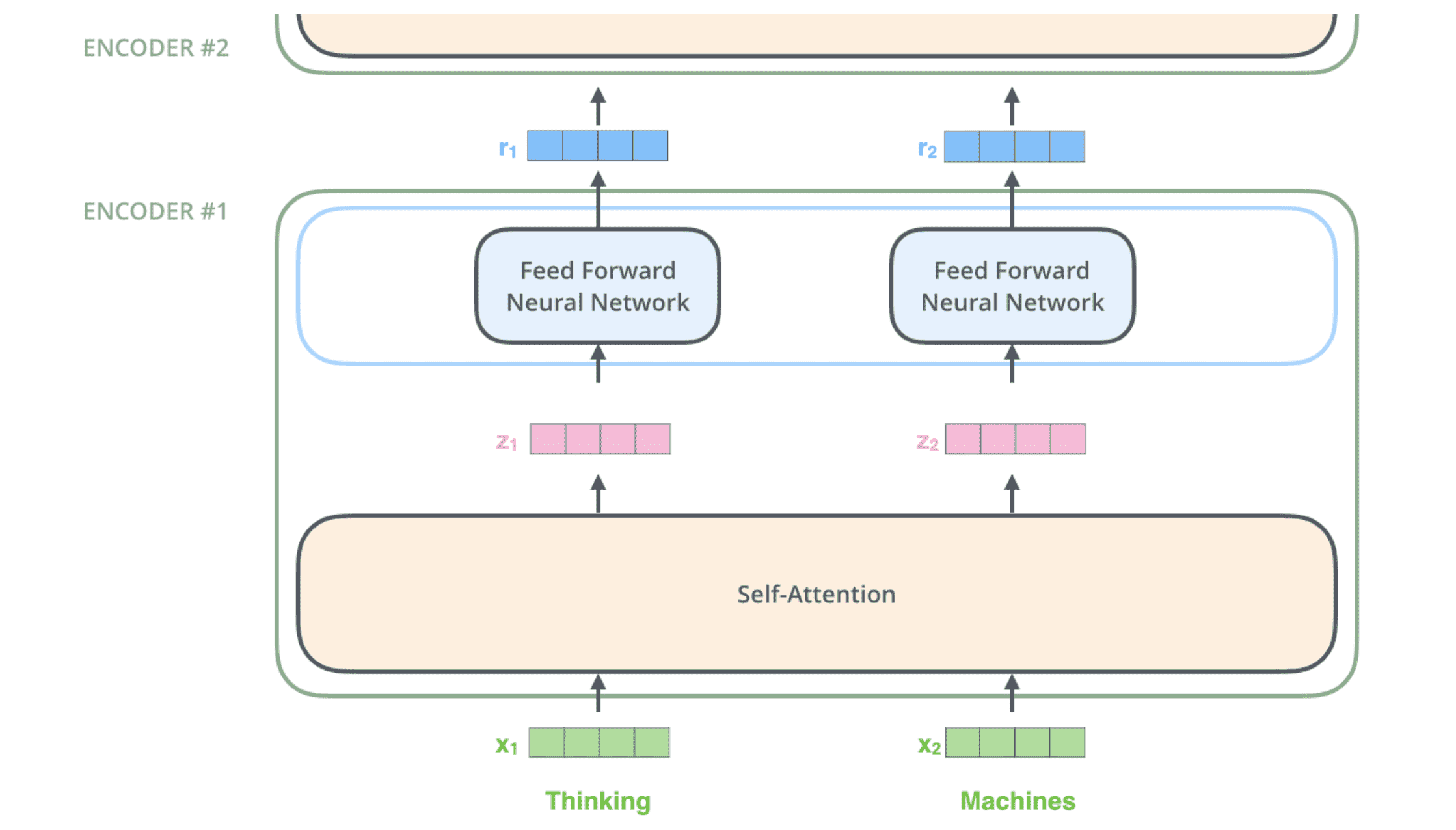
从上图可以看出，每个位置上的单词在编码器中沿着⾃⼰的路径流动。在⾃注意⼒层中，这些路径之间存在依赖关系。但是前馈层中并不存在这种相互依赖关系，因此各个词在流经前馈层时可以并⾏计算。

解码器

在 RNN 组成的 encoder-decoder 结构中，编码器把输入编码成一个统一的语义向量 context。在 Transformer 中，编码器的输出是⼀组注意向量 K 和 V，，这些将在每个解码器的 encoder-decoder attention 层中使用，帮助解码器将注意⼒集中在输⼊序列的适当位置：

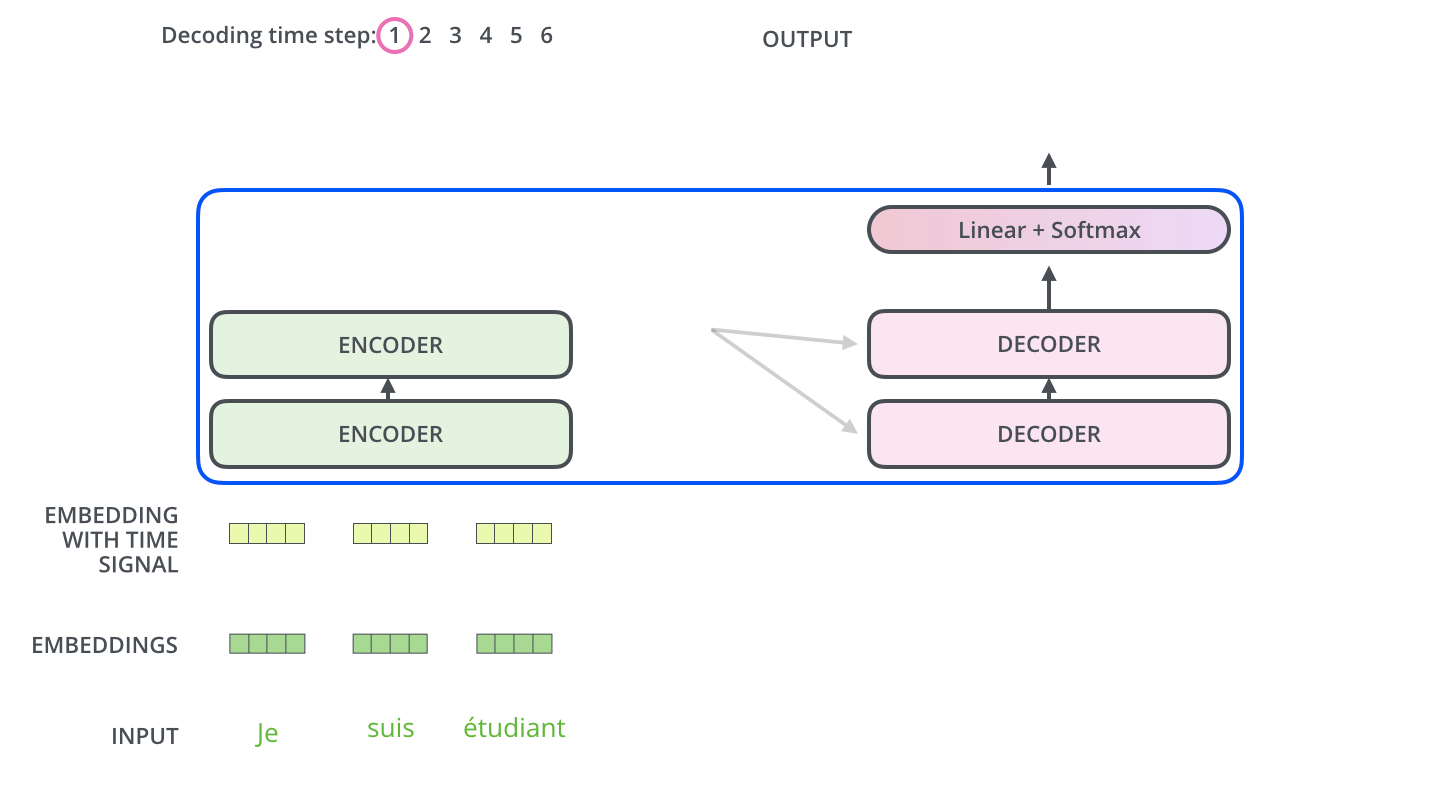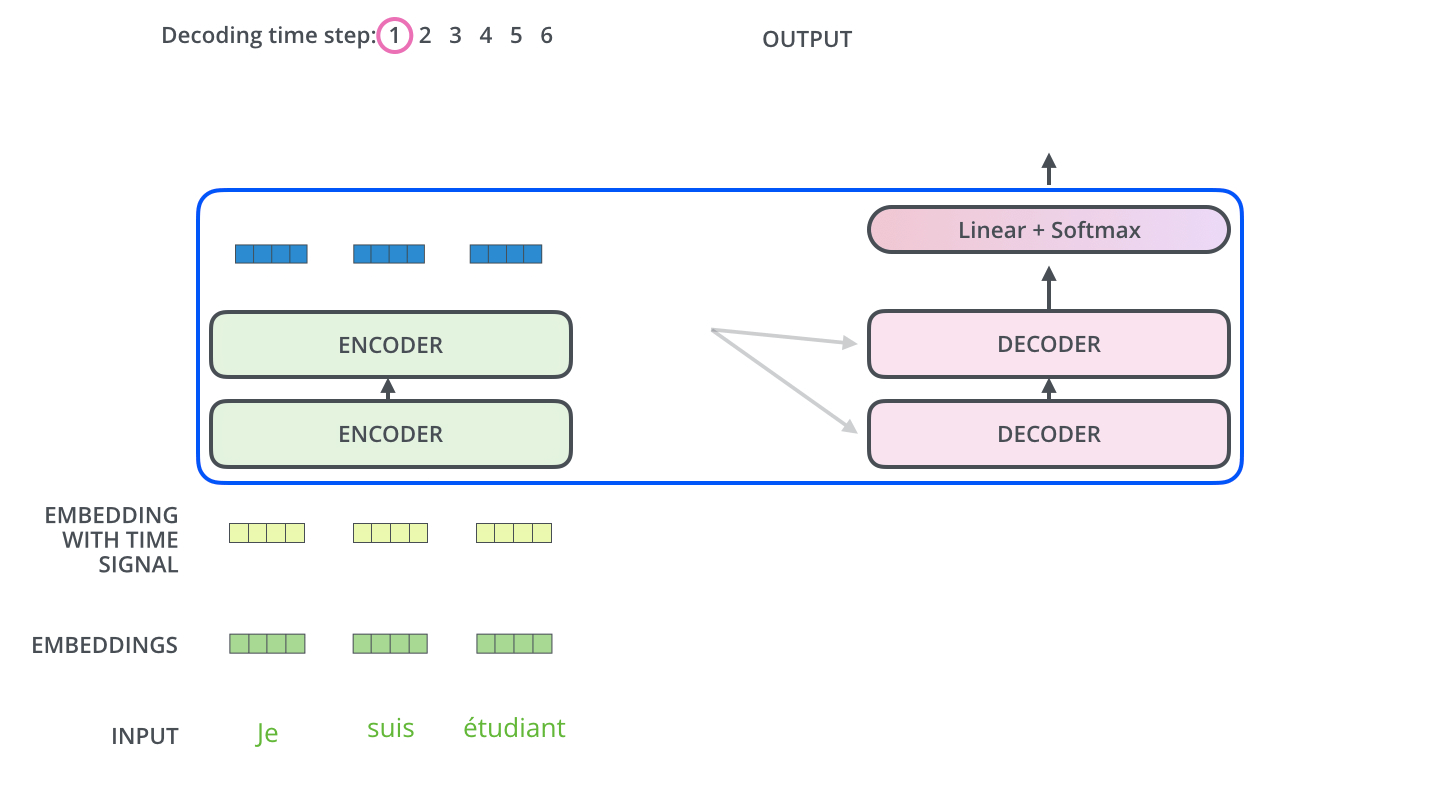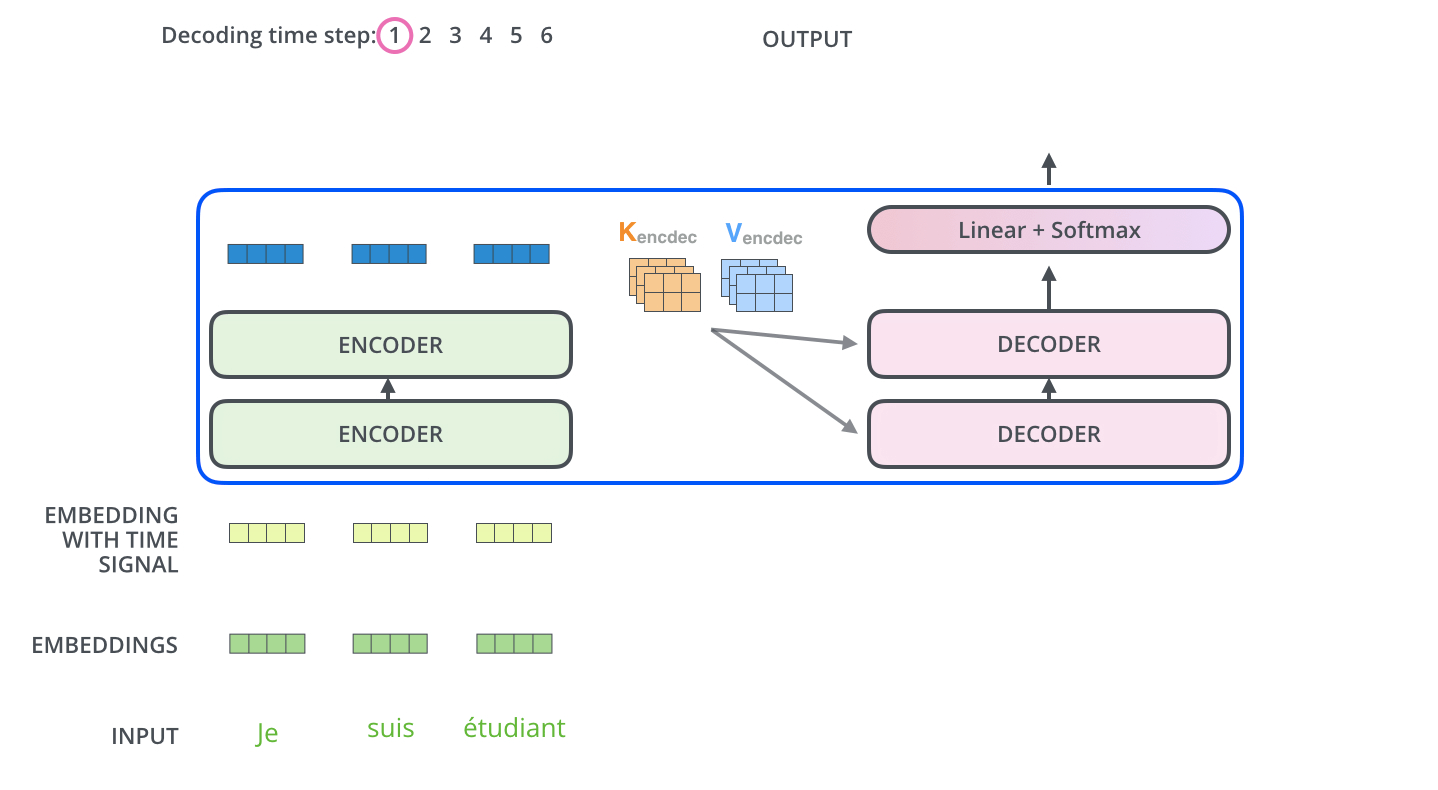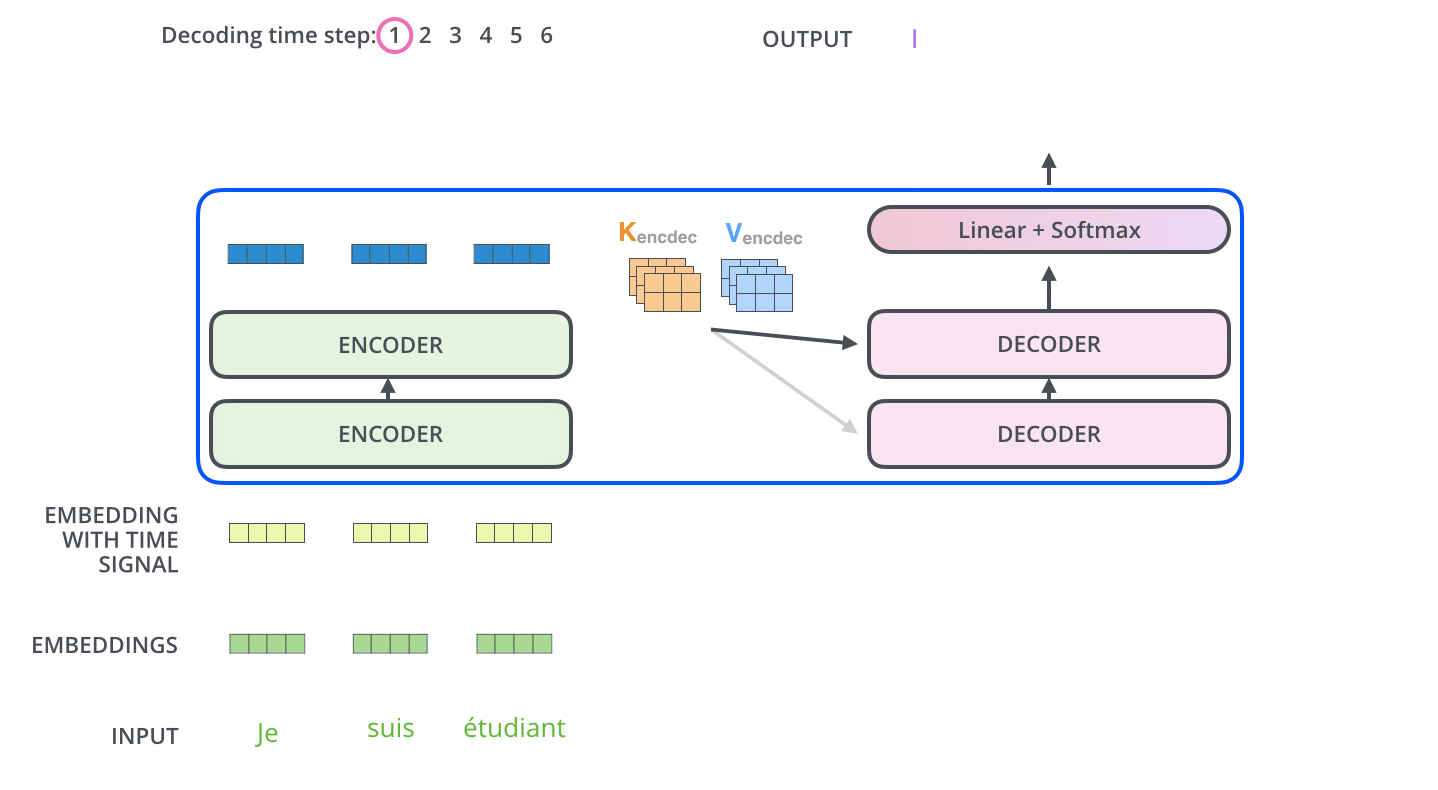
在完成编码过程之后，开始解码过程。每⼀个时间步，解码器会输出翻译后的⼀个单词：

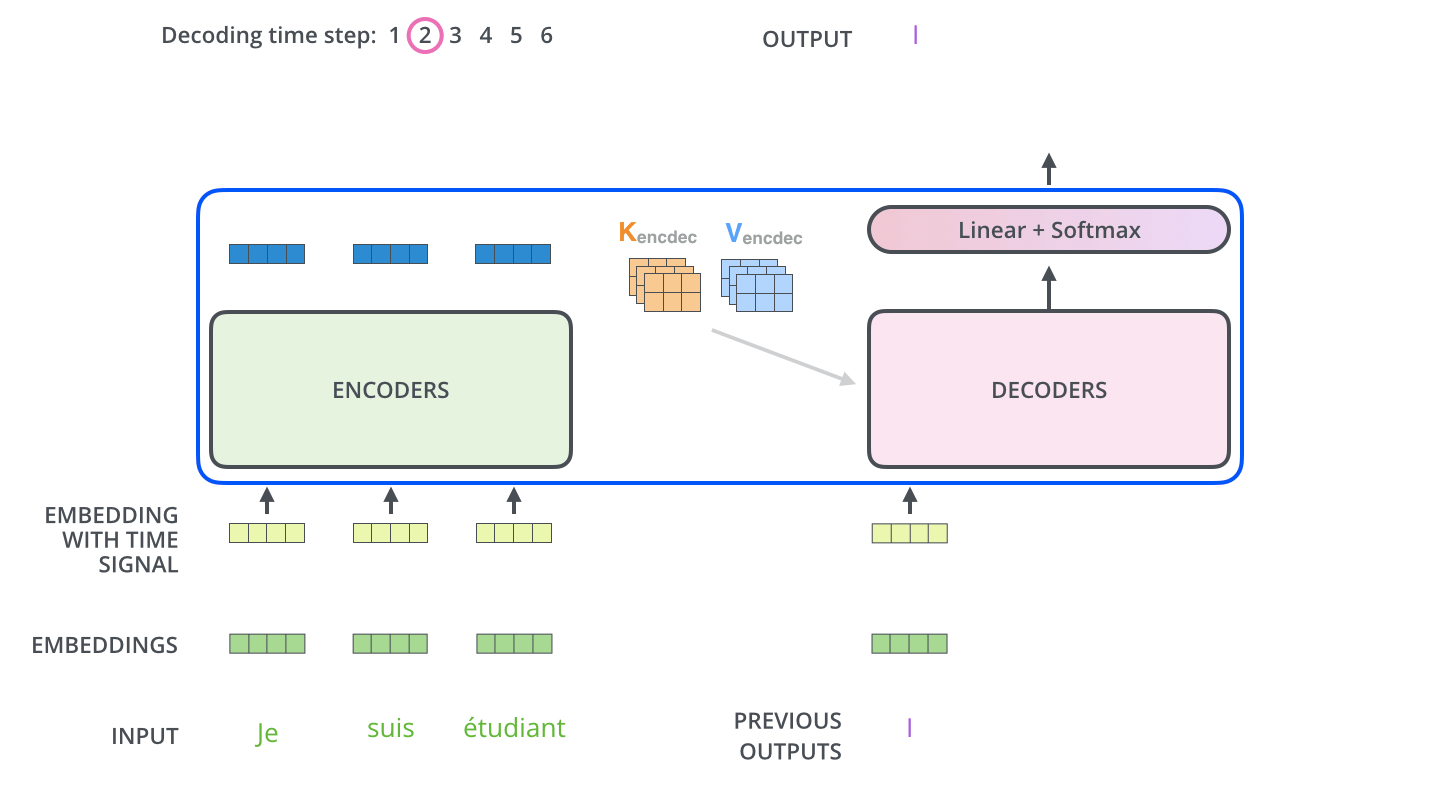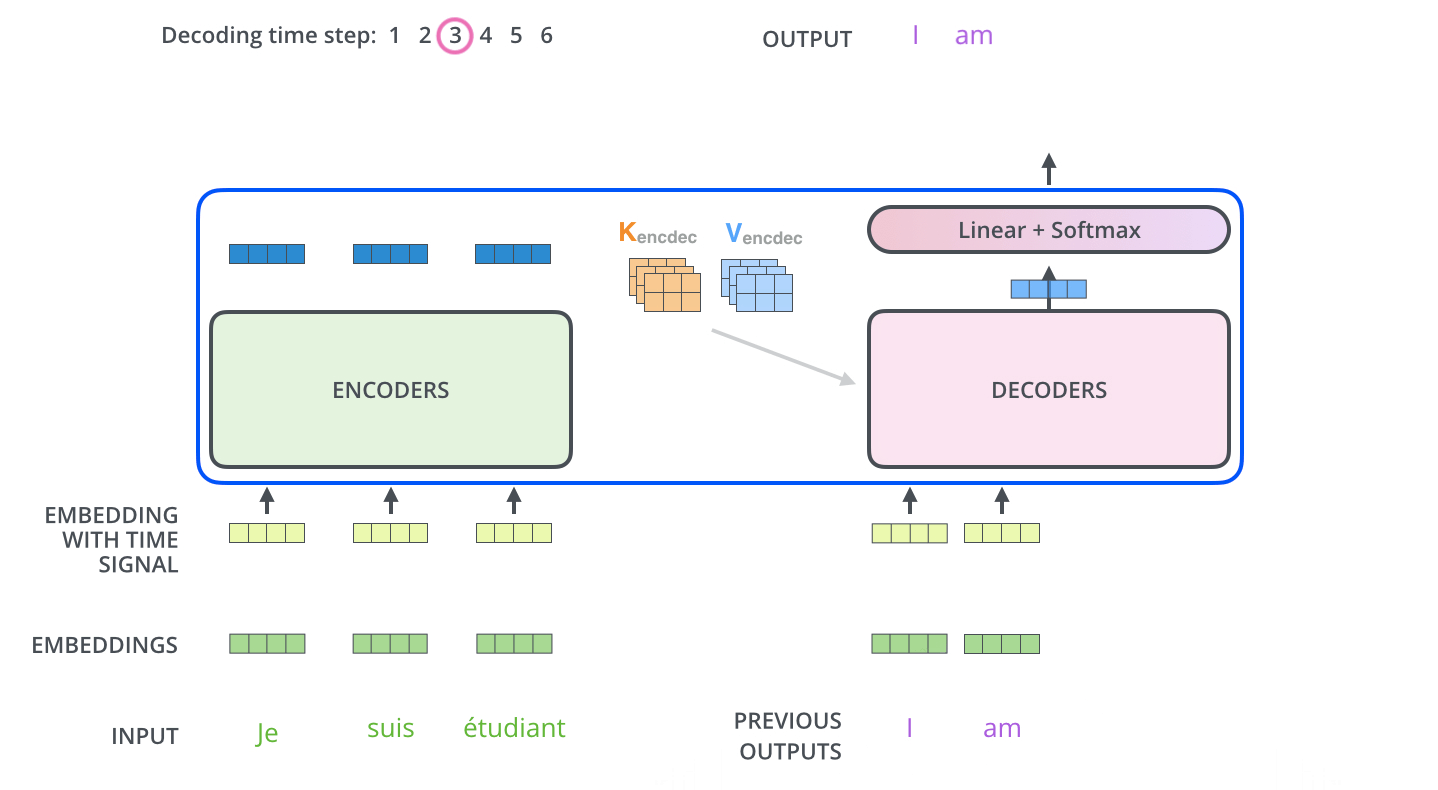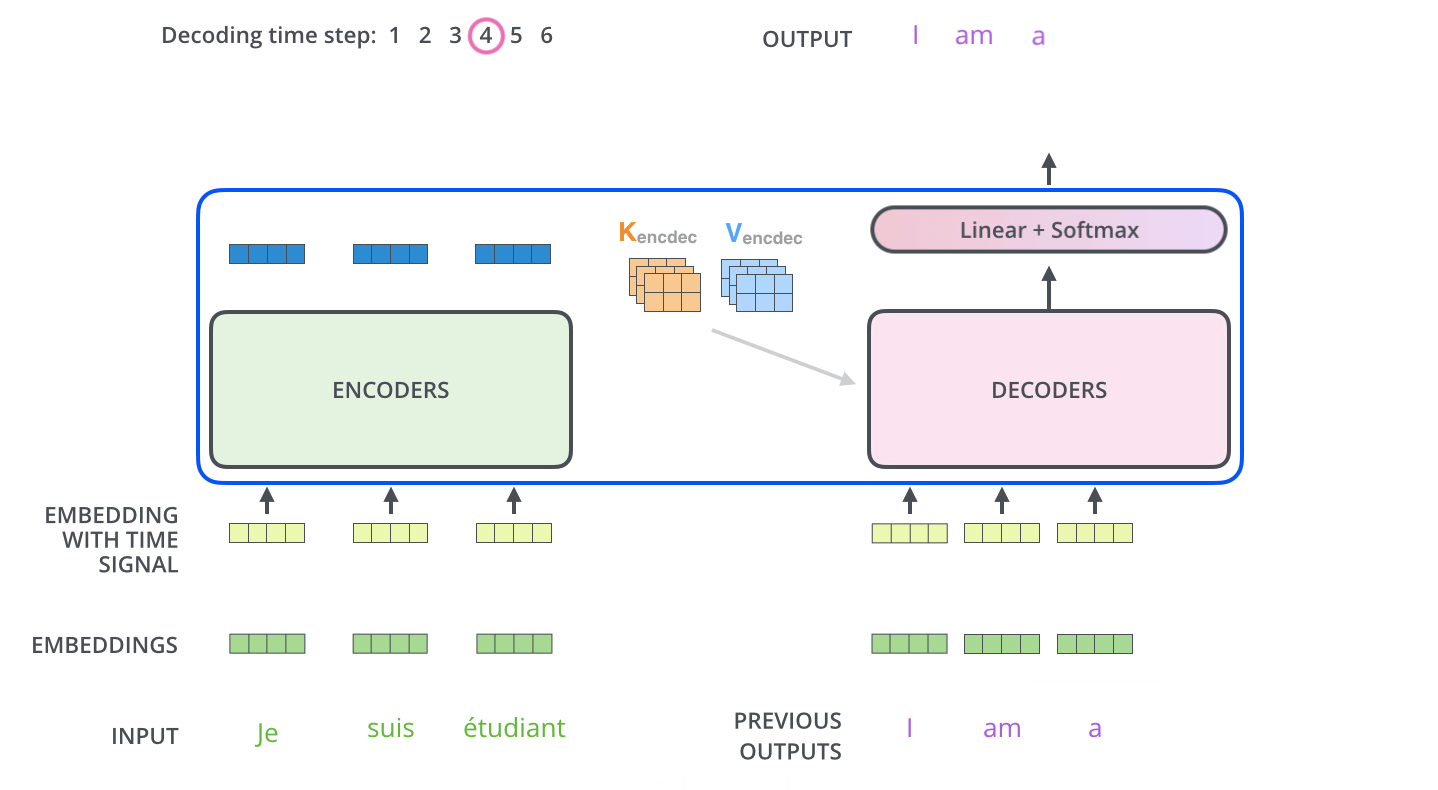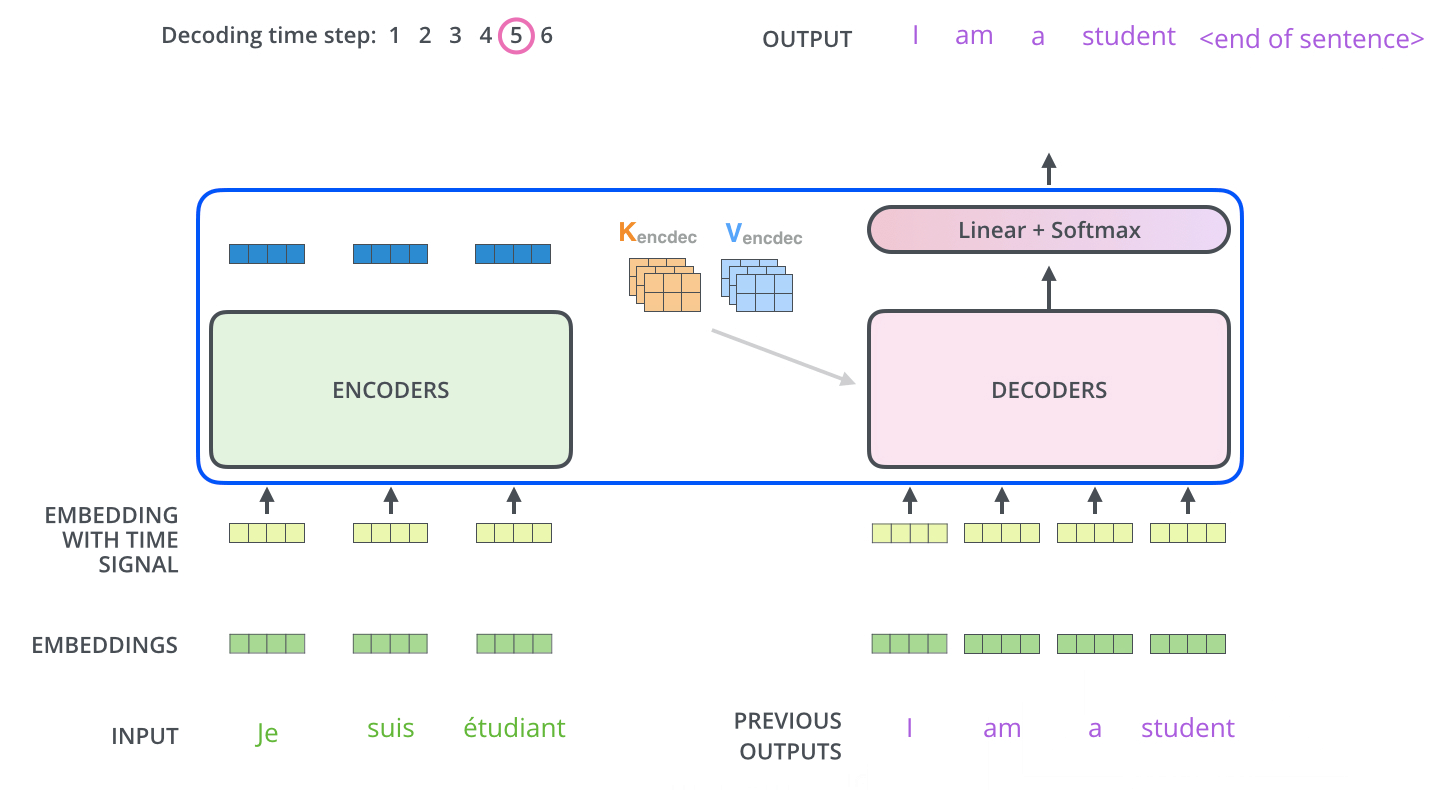
重复这样的解码过程直到出现代表结束的特殊符号。每⼀时间步的解码器输出都会在下⼀个时间步解码的时候的时候反馈给最下面的解码器，解码器就会像编码器⼀样，将该层的解码结果向更⾼层传递。

解码器中的⾃注意⼒层与编码器中的⾃注意⼒层的⼯作⽅式略有不同：在解码器中，⾃注意⼒层只允许关注到输出序列中较前的位置。也就是前面提到的 masked self-attention。Transformer 模型属于自回归模型，也就是说后面的 token 的推断是基于前面的 token 的。解码器端的 mask 的功能是为了保证训练阶段和推理阶段的一致性。在推理阶段，token 是按照从左往右的顺序推理的。也就是说，在推理 timestep=T 的 token 时，解码器只能「看到」timestep<T 的 T-1 个 token, 不能和 timestep 大于它自身的 token 做 attention 计算。

残差连接与 layer norm 层

每个编码器中的每个⼦层（self-attention）都有⼀个残差连接，同时还伴随着⼀个 layer normalization 操作：

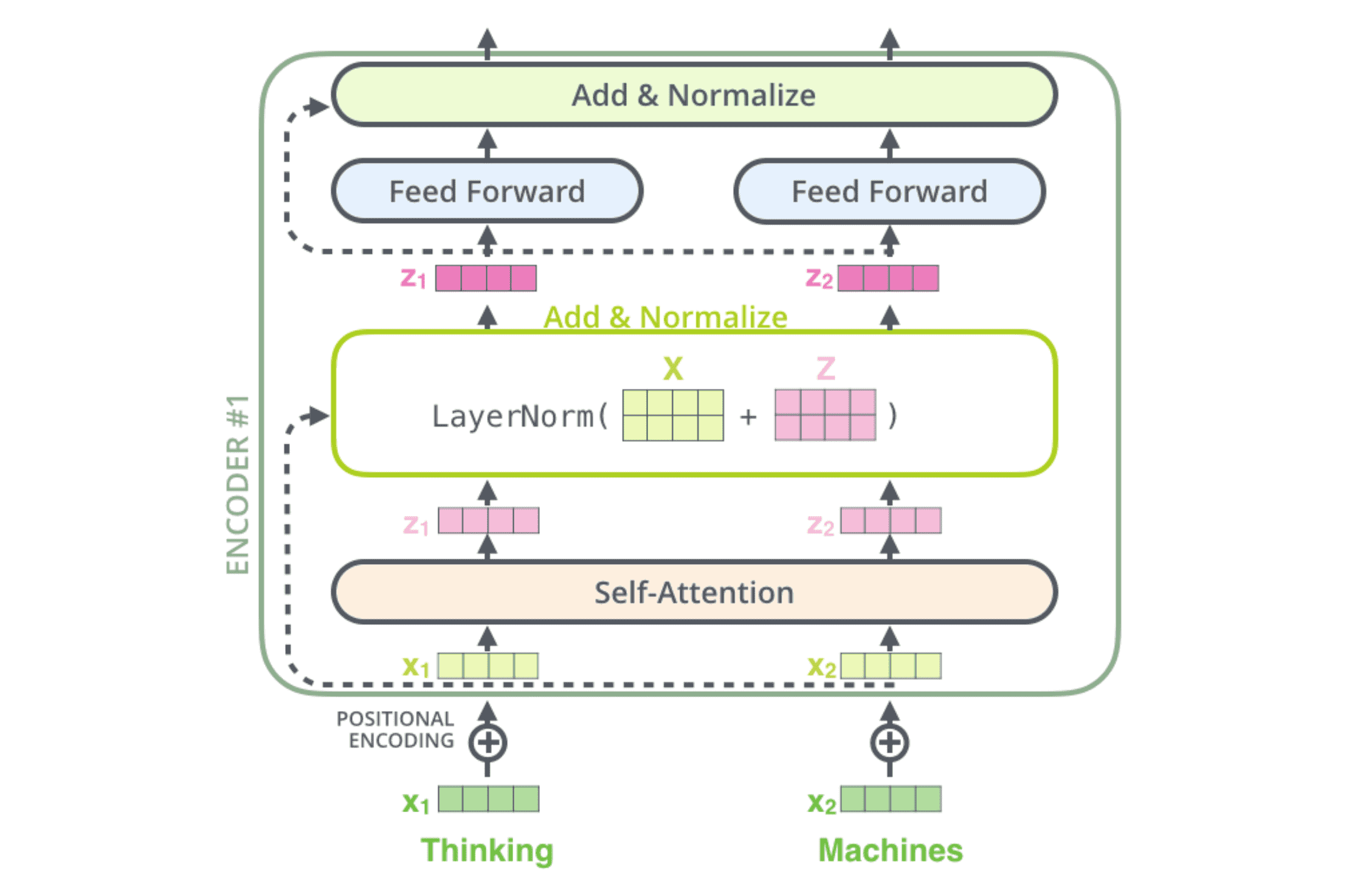
在 layer norm 层中，首先计算每个输入样本 embedding 向量的均值和方差（图中的 Input Embed 矩阵的长是 embedding 的维度，宽是输入句子的长度）：

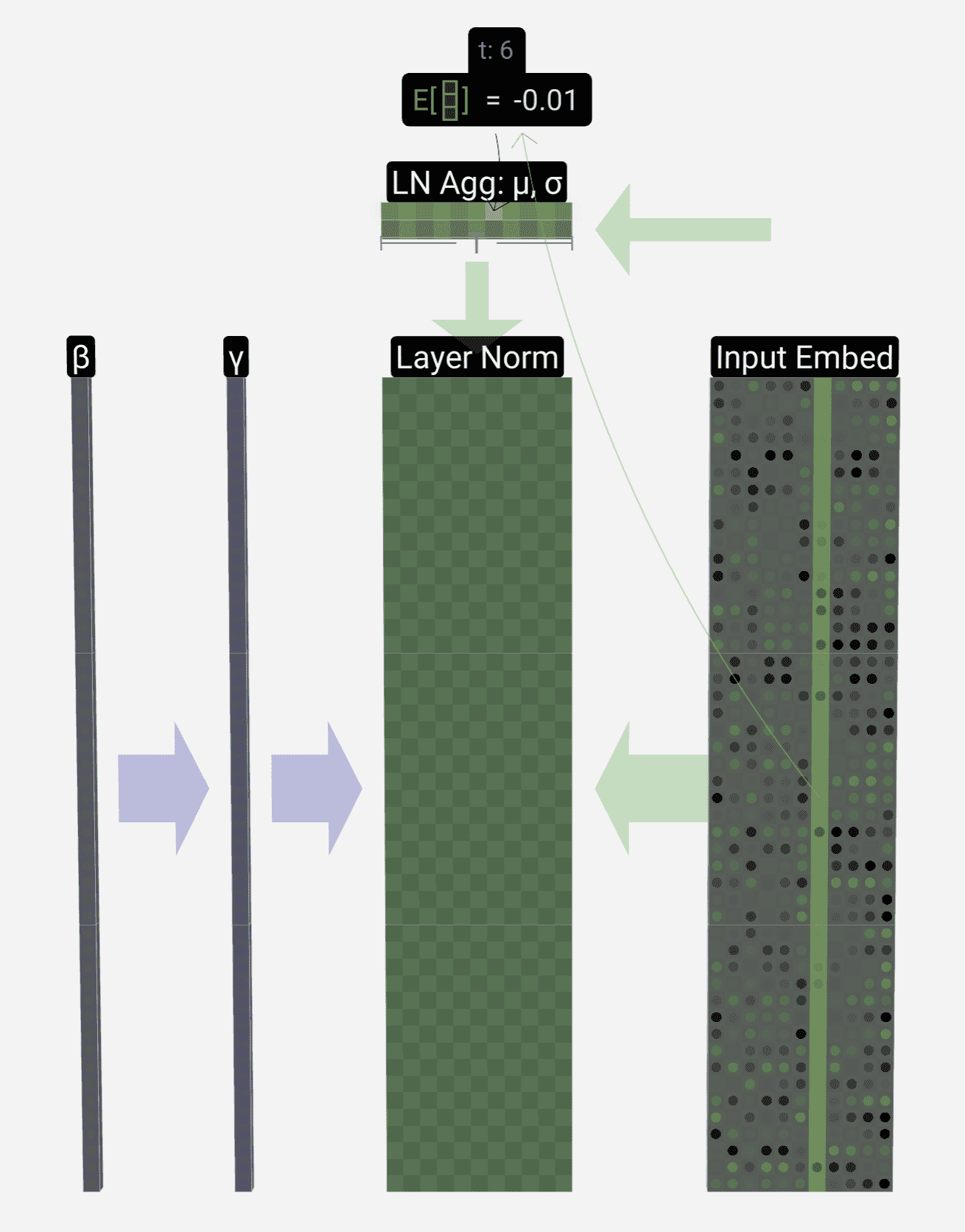
然后根据上述的均值和方差对输入 embedding 矩阵的每个元素做归一化和线性映射：

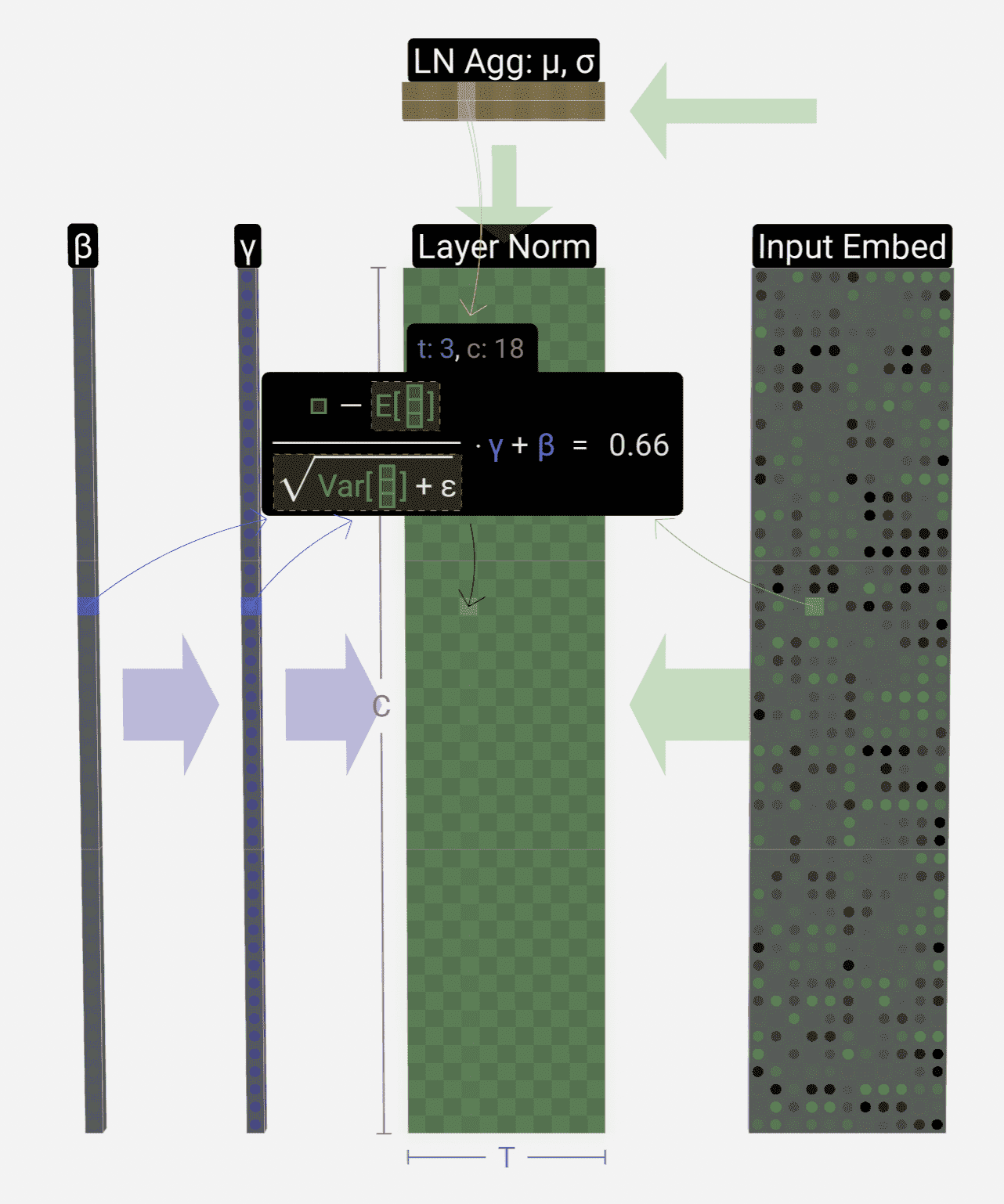
feed forward 层（MLP）

feed forward 层比较简单，是一个两层的全连接层，第一层的激活函数为 relu，第二层不使用激活函数，即：

$y = \max(W_1 \cdot x + b_1, 0) \cdot W_2 + b_2$

x 是输入，y 是输出，feed forward 层最终得到的输出矩阵的维度与输入一致。

linear 层与 softmax 层

线性层是⼀个简单的全连接层，它将解码器产⽣的向量投影到⼀个更⾼维向量（logits）上。之后的 softmax 层将这些分数转换为概率。选择概率最⼤的维度，并对应地⽣成与之关联的单词作为此时间步的输出。

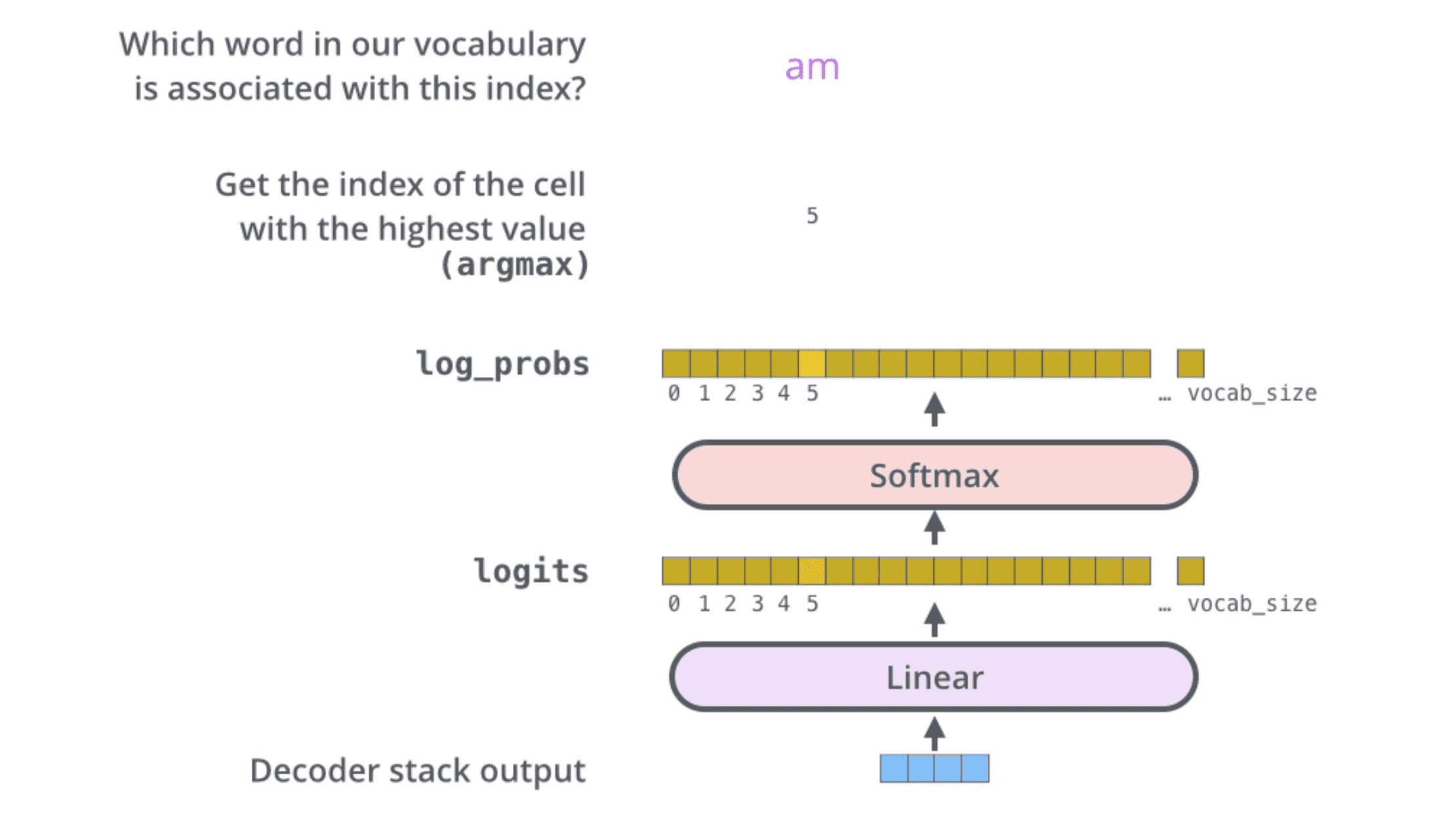
位置编码

自注意力机制无法捕捉位置信息，这是因为其计算过程具有置换不变性（permutation invariant），导致打乱输入序列的顺序对输出结果不会产生任何影响。Transformer 在解码器和编码器的输入中，使用了位置编码，使得最终的输入满足：input = input_embedding + positional_encoding。

Transformer 的位置编码采用正余弦编码：

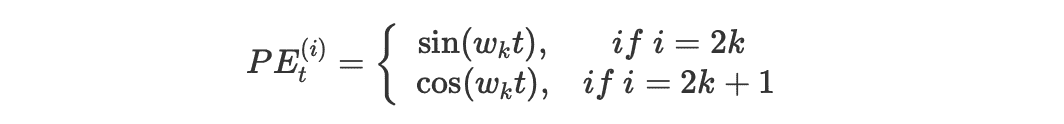
其中：

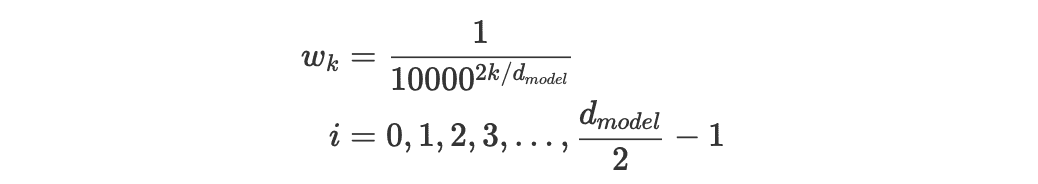
解释下几个符号的含义：

$PE_{t}$ 是这个 token 的位置编码向量，$PE_t^{(i)}$ 表示这个位置向量里的第 i 个元素
$t$ 是这个 token 在序列中的实际位置（例如第 0 个 token 为 1，第 1 个 token 为 1 等）
$d_{model}$ 是这个 token 的维度（Transformer 中是 512)

位置编码方案的演变历程可以参考《Transformer学习笔记一：Positional Encoding（位置编码）》。

GPT (Generative Pre-trained Transformers)

推理流程

正如其名字展示出来的，GPT 是由一系列的 Transformer 组成的，只不过不是前面提到的那种 encoder-decoder 结构，而是只使用了其中的 decoder。

将一个 prompt（提示词）输入 GPT，它就可以围绕一个主题生成，也即交互式条件样本生成，当然也可以仅仅给出一个开始标记 <s>。虽然说 GPT 是 Transformer-decoder 结构的，但并不是完全没有编码器，因为还是需要一个编码器来处理输入的 prompt。

输入的 promt 除了需要通过 embedding 操作，还需要加入位置编码以指示每个 token 在输入序列中的位置：

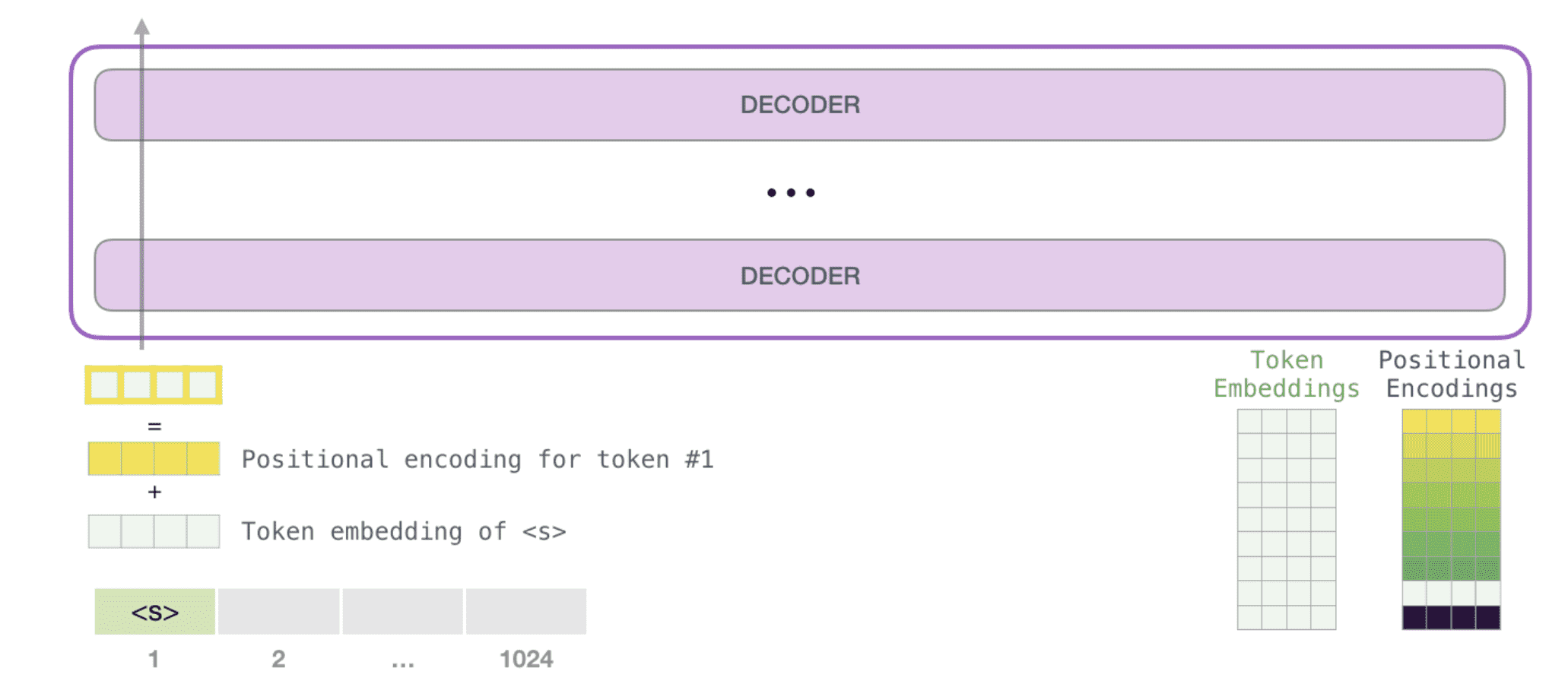
开始标记对应的向量在所有层中被连续处理：

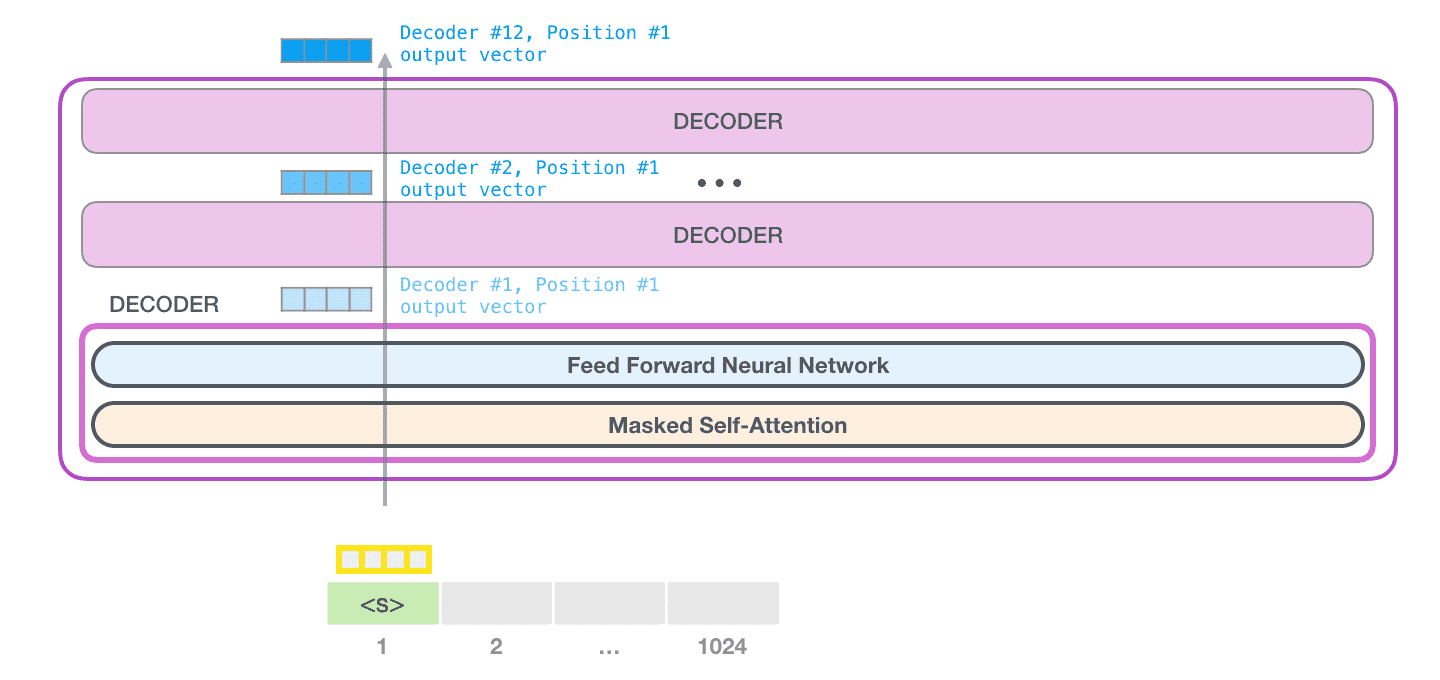
最终会产生一个概率分布向量，通过这个向量可以在词库中找到概率最大的那个词：

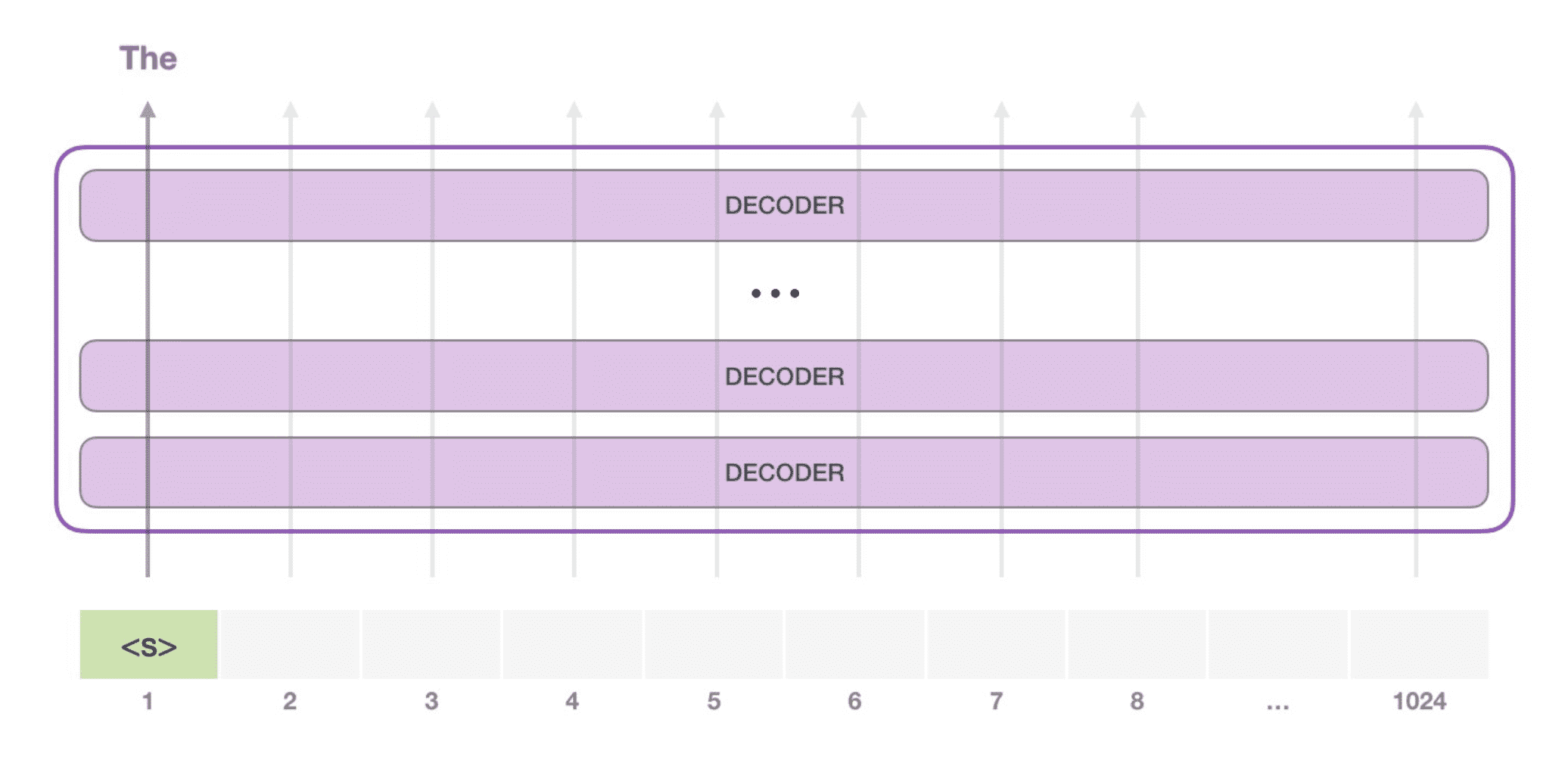
第二次推理时，会在输入 prompt 的结尾拼接上第一次推理的输出 token，然后将新的输入序列再次送入 GPT，获取到第二次输出的 token，如此重复直到 GPT 某次的输出是结束符。这就是所谓的「自回归模型」。

KV cache

在前面的推理过程中，每一轮迭代输入一个 token 序列，经过 embedding 层将输入序列变为一个三维张量 [b, s, h]（b 是 batch size，s 是输入序列的长度，h 是 embedding 维度），然后该张量通过 $W^Q, W^K, W^V$ 三个权重张量变换成 Q, K, V 三个张量。

当前轮输出 token 与输入 token 序列拼接，并作为下一轮的输入 token 序列，反复多次。可以看出前一轮的输入数据只比当前轮输入数据新增了一个 token，其他全部相同。因此当前轮推理时必然包含了前一轮的部分计算。KV cache 的出发点就在这里，缓存当前轮可重复利用的计算结果，下一轮计算时直接读取缓存结果。通过名字就能看出来，KV cache 指的就是缓存每一轮迭代中的 K 张量和 V 张量。当然随着迭代轮数的增加，KV 张量的尺寸也会变化（对应序列长度维度的变化），所以每一轮迭代中都需要更新 KV cache，即将新的 KV 向量拼接到旧的 KV 张量上。

GPT 在进行推理时，主要包括两个步骤：

1. prefill

在 prefill 步骤中，输入 prompt 对应的 K、V 矩阵会被计算并缓存下来。因为每一个 decoder 层都有自己的 $W^Q, W^K, W^V$，所以在这一步中，每一层的 K 和 V 会被计算并缓存。每一个请求的 prompt 需要经过这个阶段，只计算一次。

2. decoding

生成新 token 阶段是串行的，具体包括两步：

查询 KV cache，计算并输出当前 token 最终 embedding 用来预测下一个 token
缓存计算过程中得到的当前 token 在每一层的 K 和 V，拼接到 prefill 阶段中的 KV cache 中

KV cache 的好处是每次解码不需要对整个网络全部进行计算。prefill 只需要计算一次，核心就是 GPT-style 的 Transformer 是单向的，而不是双向的：每一个 token 只与它前面的 tokens 有关系，其 KV 也只与其前面的 tokens 有关系，因此可以只计算一次且可以并行。