2024-01-13发表2024-02-25更新深度学习算法10 分钟读完 (大约1536个字)0次访问

FlashAttention 原理 | 深度学习算法

FlashAttention 的计算结果和原始算法是严格对齐的，不是对 attention 进行近似。FlashAttention 通过分块的方式减少对全局内存的读写，从而加速运算过程。本文仅包含对 FlashAttention 在前向推理上的优化，不包含反向传播相关内容。

softmax 分块

attention 的运算过程中包括矩阵乘法和 softmax 运算。矩阵乘法的分块方式比较成熟，但是 softmax 因为涉及到了全局信息所以分块计算比较困难，本节将推导 softmax 分块运算的方式。

original softmax

原始 softmax 的公式和伪代码如下：

$$y_i=\frac{e^{x_i}}{\sum_{j=1}^Ve^{x_j}}$$

可以看出，访存的开销是 2 次 load 和 1 次 store。

safe softmax

在实际硬件上，所表示的数字范围是有限的，Algorithm 1 的第 3 行可能会由于指数而上溢或下溢。safe softmax 的公式和伪代码如下：

$$y_i=\frac{e^{x_i-\max_{k=1}^Vx_k}}{\sum_{j=1}^Ve^{x_j-\max_{k=1}^Vx_k}}$$

可以看出，访存的开销是 3 次 load 和 1 次 store。

online softmax

online softmax 算法可以减少 safe softmax 算法的访存次数，先直接看伪代码：

Algorithm 3 的 1～6 行在一次访存中同事计算出了最大值 $m_V$ 和指数和 $d_V$，其中第 5 行可以通过数学归纳法证明：

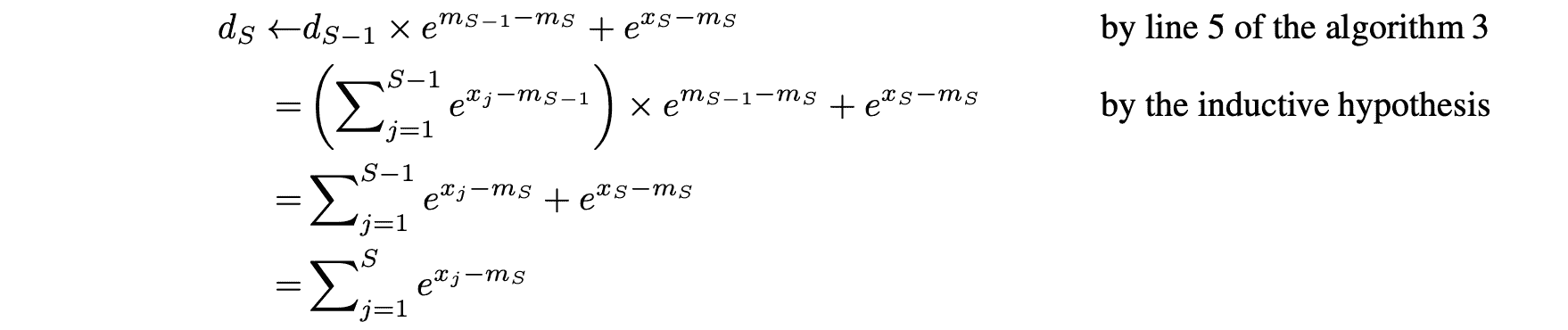
可以看出，访存的开销是 2 次 load 和 1 次 store。

tiled softmax

QKV 矩阵乘法分块

整体流程

先回顾一下 attention 的计算方式：

换成流程图描述下：

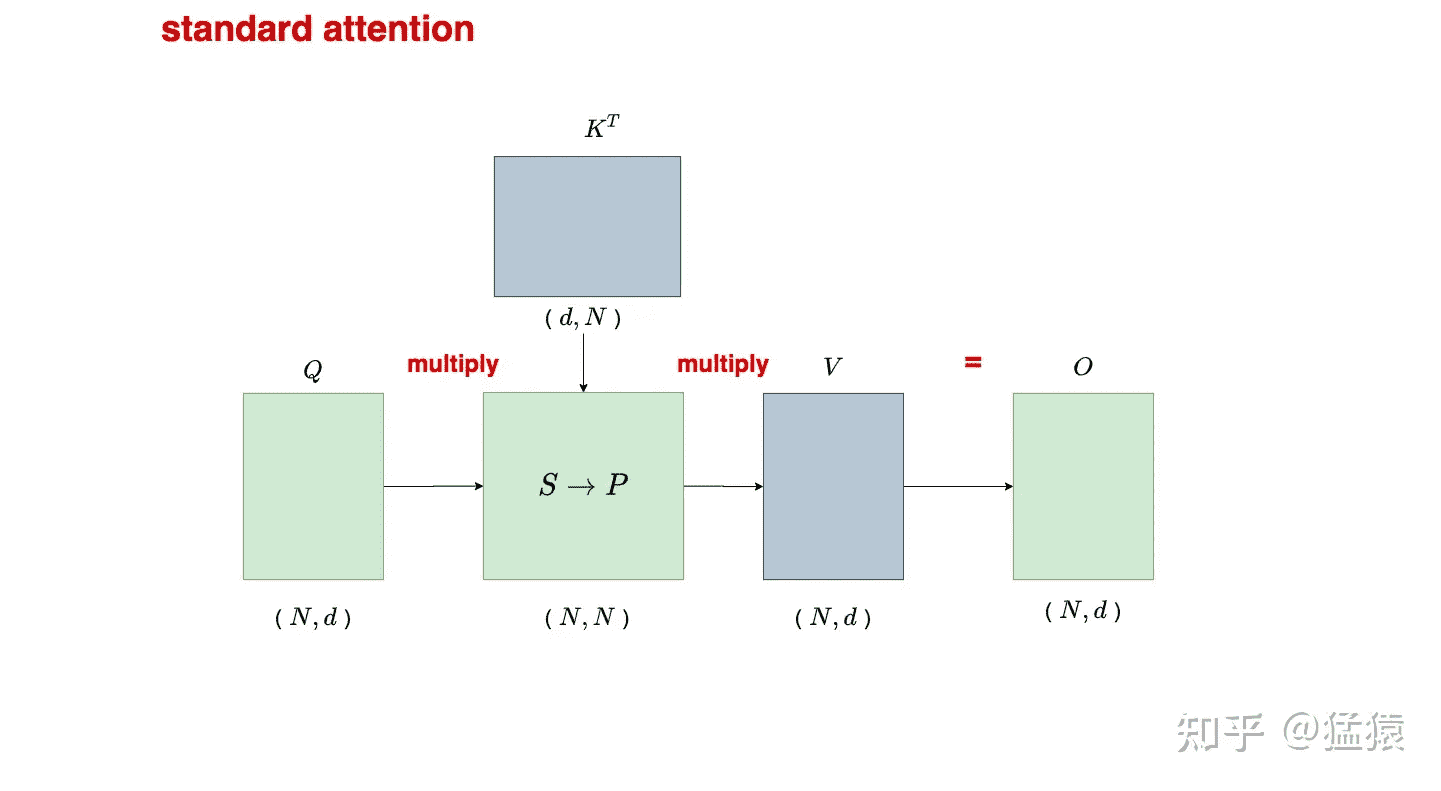
其中 $P=softmax(S)$，示意图如下：

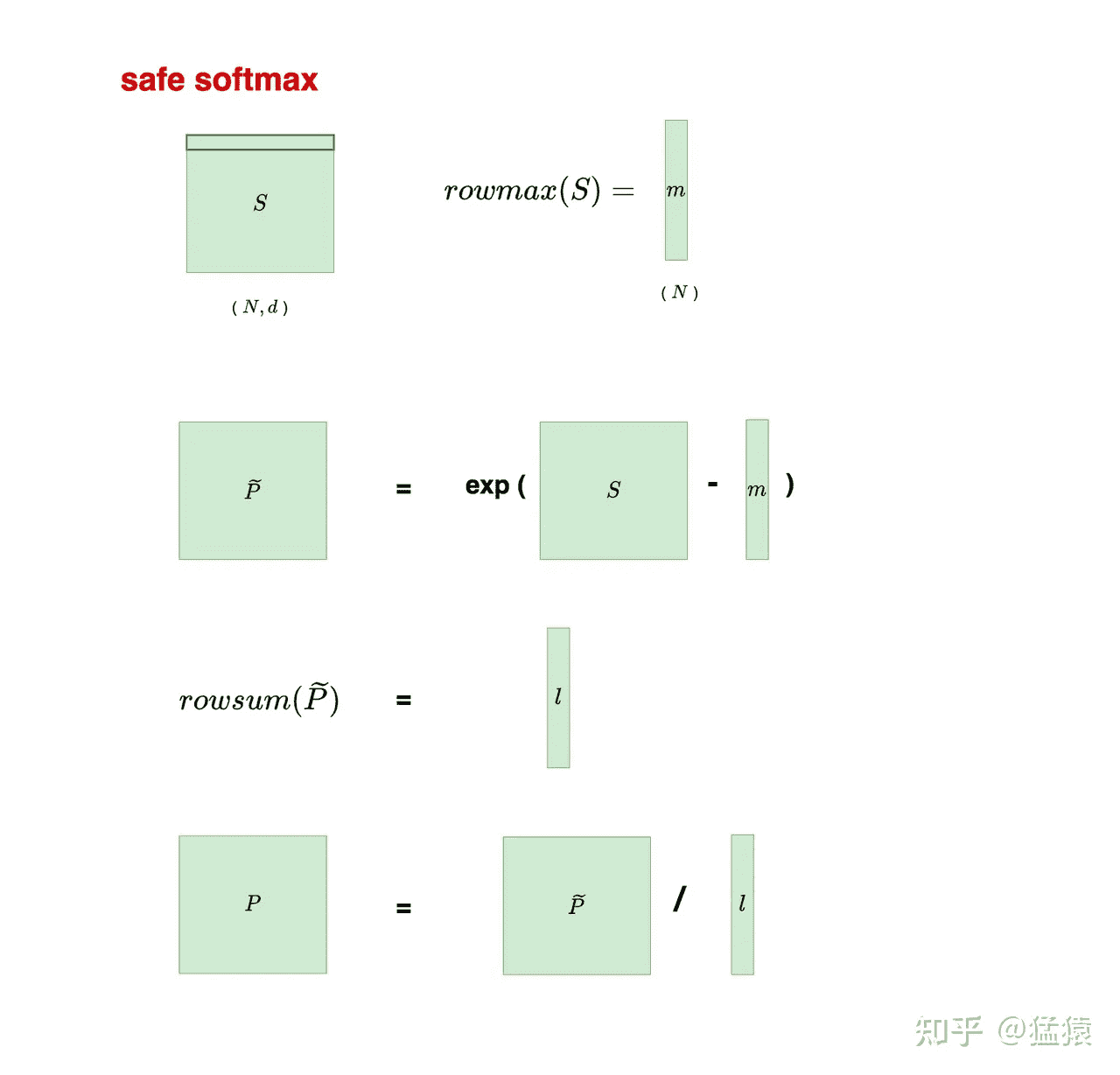
注意这里矩阵每一行是一个样本，每个样本之间是独立的，所以在求最大值和以及求和的时候是针对每一行的。

在 GPT 类的模型中，还需要对 P 做 mask 处理。为了表达方便，诸如 mask、 dropout 之类的操作都忽略掉。

分块运算

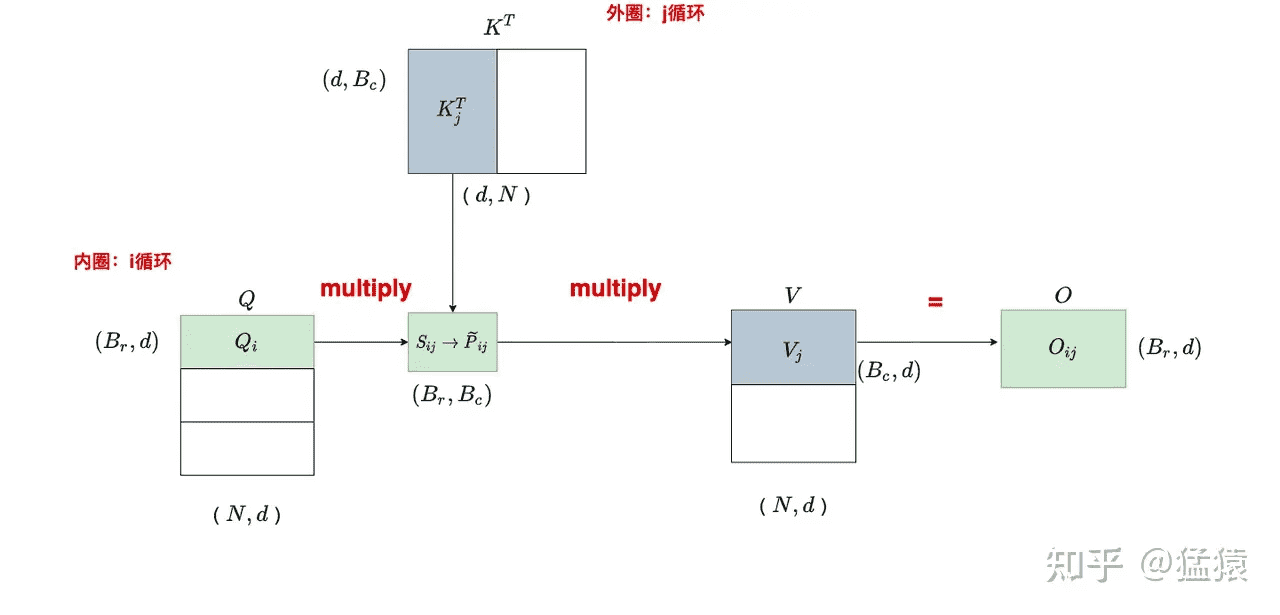
j = 0 时，遍历 i：

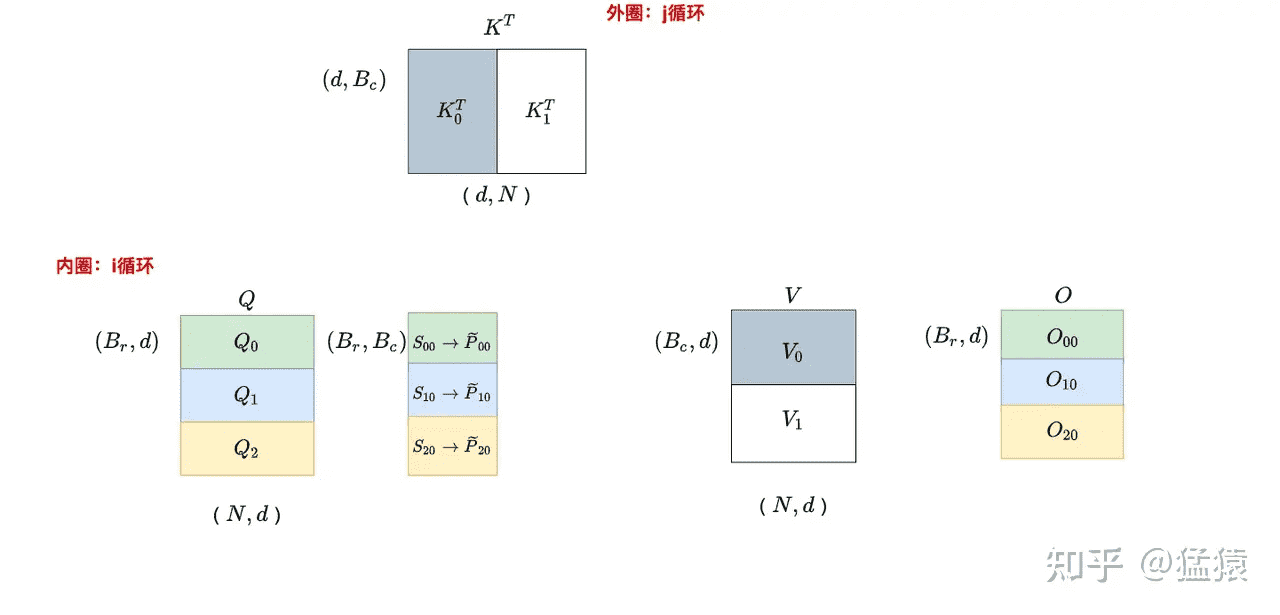
j = 1 时，遍历 i：

整个计算过程分为两层循环，内层循环是 i，外层循环是 j。在 $S_{ij}=Q_iK_j^T$ 的计算过程中，$S_{ij}$ 是不需要反复读写的（因为没有在 k 方向上做切分），进而 $\widetilde{P}{ij}$ 也不需要反复读写。而在 $O{ij}=\widetilde{P}{ij}V_j$ 的计算过程中，$O{ij}$ 是需要反复读写进行累加的。虽然 $\widetilde{P}{ij}$ 不需要反复读写，但是其每个分块的结果不是我们最终想要的结果（因为使用的是每个分块的局部 softmax 结果），又因为 $O{ij}$ 需要反复读写，所以将局部 softmax 结果更新成全局结果的操作就放在 $O_{ij}$ 的计算中一起完成。所以，分块计算 softmax 的意义就是省去对 $S$、$P$ 的读写。

更新输出

和前面提到的 online softmax（注意不是 tiled softmax）类似，我们希望能够找出一个方法，可以在迭代中更新 $O_i$，即通过 $O_{i-1}$ 得到 $O_i$。

注意这里的 $O_i^{(j+1)}$ 是 $O$ 每个分块的最终结果，而不是需要加在一期的部分结果。三个变量对应的部分如下所示：

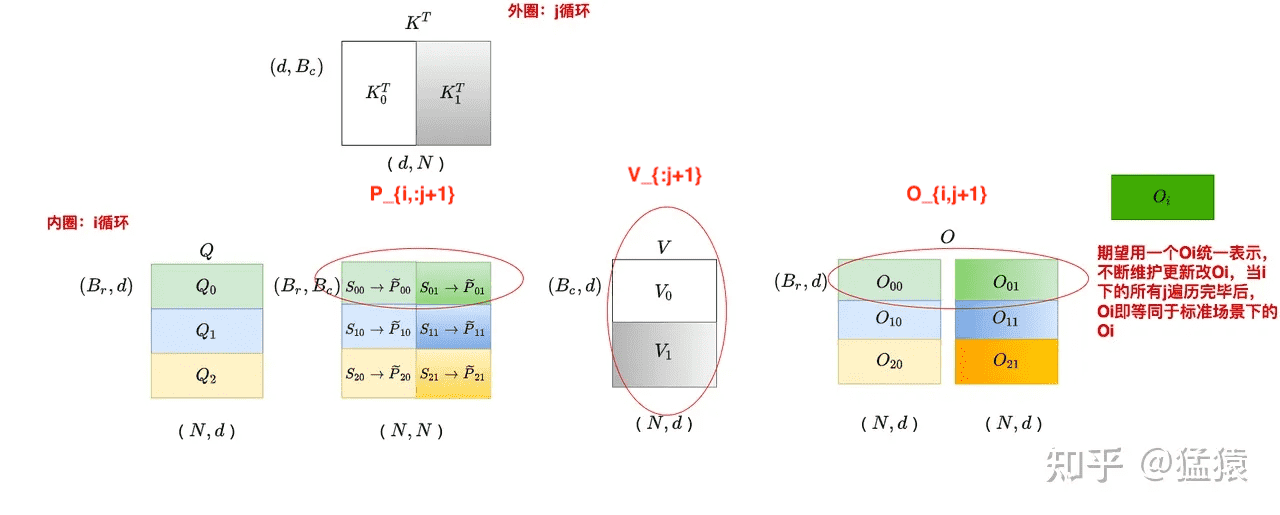
现在再回头看原论文中的伪代码就比较清楚了：

GPU 显存分布情况

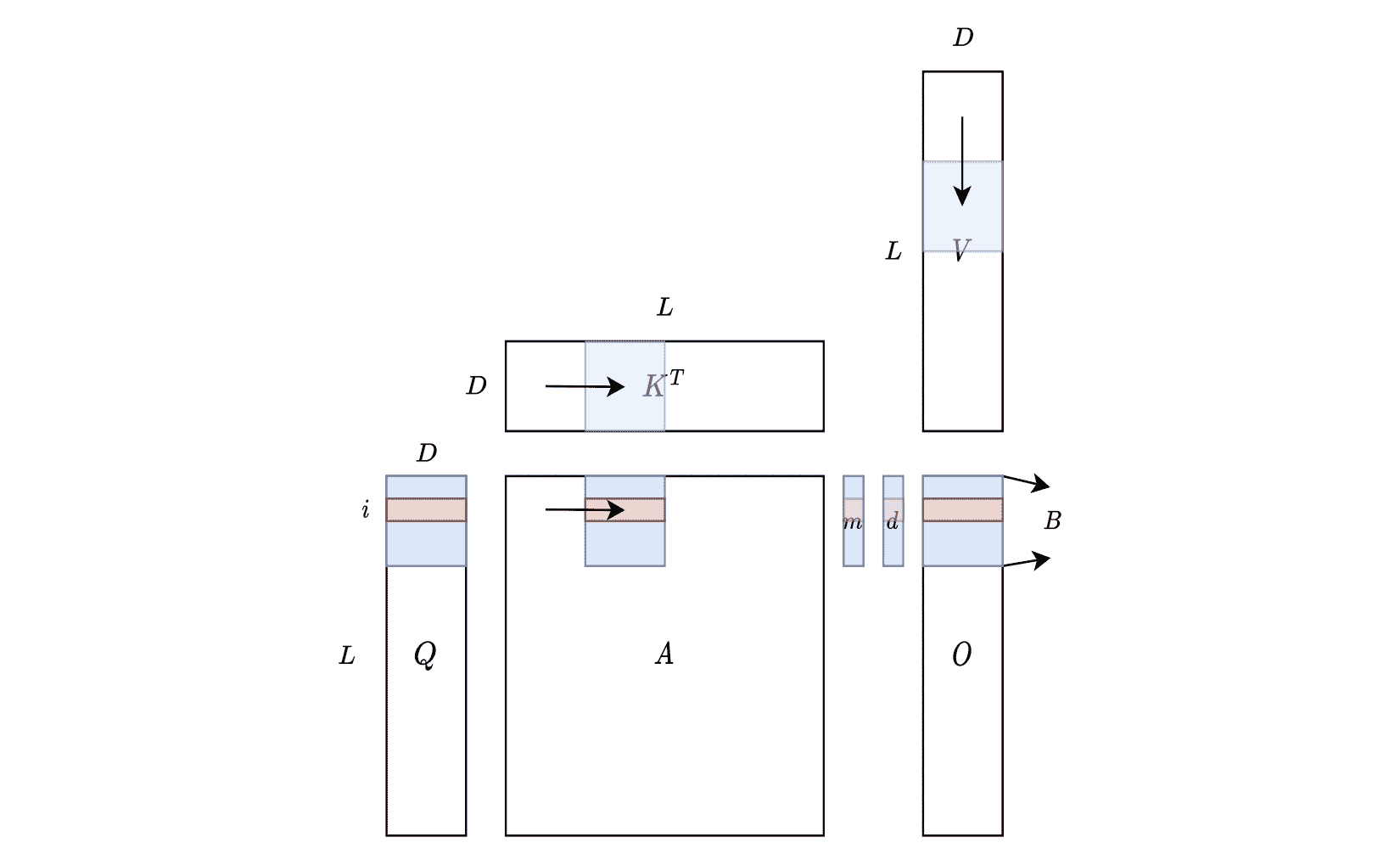
上图说明了 FlashAttention 如何在硬件上计算。蓝色块代表驻留在 SRAM 中的块，而红色块对应于第 $i$ 行。 $L$ 表示序列长度（即前文中的 $N$），可以很大（例如 16k），$D$ 表示注意力头的尺寸（即前文中的 $d$），在 Transformers 中通常很小（例如 GPT-3 为 128），$B$（即前文中的 $B_r$）是可以分块的大小。值得注意的是，总体 SRAM 内存占用仅取决于 $B$ 和 $D$，与 $L$ 无关。因此，该算法可以扩展到长上下文而不会遇到内存问题（GPU 共享内存很小，H100 架构为 228kb/SM）。在计算过程中，从左到右扫描 $K^T$ 和 $A$，从上到下扫描 $V$，并相应地更新 $m$、$d$（即前文中的 $l$）和 $O$ 的值。

复杂度分析

计算复杂度

FlashAttention 的计算复杂度可以通过原论文中的伪代码进行分析:

根据伪代码第 9 行 $S_{ij}=Q_iK_j^T$，其中 $Q_i\in\mathbb{R}^{B_rd},K_j^T\in\mathbb{R}^{dB_c}$，可以得出 $S_{ij}$ 的计算复杂度是 $O(B_rB_cd)$
同理根据伪代码第 12 行，可以得出 $\tilde{P}_{ij}V_j$ 的计算复杂度也是 $O(B_rB_cd)$
循环一共执行了 $T_cT_r=\frac N{B_c}\frac N{B_r}$ 次

综上可以得出 FlashAttention 的计算复杂度是 $O(\frac{N^2}{B_cB_r}B_rB_cd)=O(N^2d)$。