OpenCV 如何实现双线性插值缩放 | 系统开发

本文介绍了如何 OpenCV 实现双线性插值缩放的算法细节。

背景

最近在做一些视觉算法的跨平台移植，视觉算法移植中的一个环节是数据对齐，就是保证对于相同图片的输入，不同平台程序输出的结果是一致的。视觉算法整个流程可以分为三步：前处理、网络推理、后处理。其中后处理多是一些算法强相关逻辑，多为代码直接实现，移植难度不大（直接复制过来即可）。网络推理部分的数据对齐性则由负责推理引擎开发的同学保证。这样一来，我的关注点则多在如何正确的实现和原来平台行为一致的预处理操作。

一般来说，跑在服务器端的视觉算法的预处理步骤多使用 OpenCV 完成。但是我手头的一个算法当初在开发的时候，为了满足性能的要求，在对图片进行缩放的时候，没有使用 OpenCV 提供的 resize 函数，而是使用 CUDA 自己实现了一个 resize 函数，插值算法使用的是双线性插值。移植的时候我就直接使用了 OpenCV 提供的 resize 函数来替换之前的开发者写的 CUDA resize 函数。但是却发现出现了数据对不齐的情况，经过排查发现是 resize 函数的问题。我仔细看了 CUDA resize 函数，逻辑比较简单，就是实现了一个双线性插值的缩放操作，但是却和 OpenCV 的 resize 结果不一致。这就说明 OpenCV 在实现逻辑上并不是简单地计算插值，这个差异只能在源码中找到。

双线性插值缩放

先介绍一下双线性插值的基本原理和计算流程。

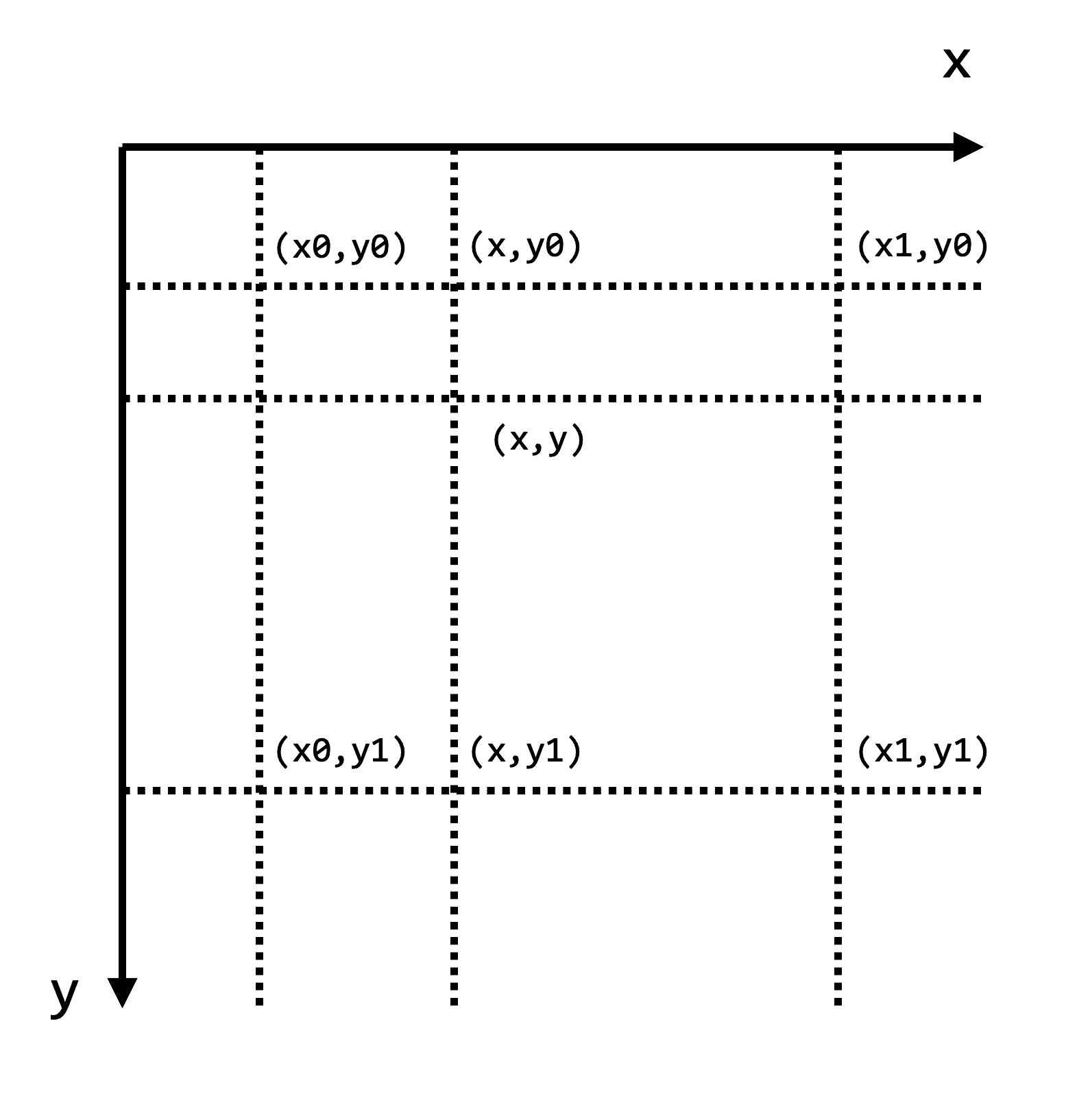
对于缩放后的图片的每一个像素值 src_img[x, y]，都可以根据缩放系数计算出其在原图中的对应位置 (x*scale_x, y*scale_y)，但是这个位置往往不是恰好落在原图的某个坐标上，而是落在了四个坐标的中间，这就需要通过线性映射的方式估计出这个点的像素值。

如上图所示，已知周围四个点的像素值，求位于坐标 (x,y) 出的像素值，需要先求出 x 方向上两个点的像素值，即先在 x 方向上进行两次线性插值，计算公式为：

$$
f(x, y_0) = \dfrac{x_1-x}{x_1-x_0} f(x_0,y_0) + \dfrac{x-x_0}{x_1-x_0} f(x_1,y_0)
$$

$$
f(x, y_1) = \dfrac{x_1-x}{x_1-x_0} f(x_0,y_1) + \dfrac{x-x_0}{x_1-x_0} f(x_1,y_1)
$$

然后在 y 方向上进行线性插值，便可以得到最终的输出：

$$
\begin{aligned}
f(x,y) &= \dfrac{y_1-y}{y_1-y_0} f(x, y_0) + \dfrac{y-y_0}{y_1-y_0} f(x, y_1) \
&= \dfrac{1}{(x_1-x_0)(y_1-y_0)}(f(x_0,y_0)(x_1-x)(y_1-y)+f(x_1,y_0)(x-x_0)(y_1-y)+f(x_0,y_1)(x_1-x)(y-y_0)+f(x_1,y_1)(x-x_0)(y-y_0))
\end{aligned}
$$

由于 (x,y) 周围的四个点是相邻的，所以 $x_1-x_0=1, y_1-y_0=1$，所以上式可以变为：
$$
\begin{aligned}
f(x,y) &= f(x_0,y_0)(x_1-x)(y_1-y)+f(x_1,y_0)(x-x_0)(y_1-y)+f(x_0,y_1)(x_1-x)(y-y_0)+f(x_1,y_1)(x-x_0)(y-y_0) \
&= a_0f(x_0,y_0) + a_1f(x_1,y_0) + a_2f(x_0,y_1) + a_3f(x_1,y_1)
\end{aligned}
$$
其中，$a_0=(x_1-x)(y_1-y)$，$a_1=(x-x_0)(y_1-y)$，$a_2=(x_1-x)(y-y_0)$，$a_3=(x-x_0)(y-y_0)$。

可以看出来，$a_{0-4}$ 分别是点 (x,y) 四周四个矩形的面积。直观点说的话，待求点的像素值 = 左上点的像素值 x 右下矩形的面积 + 左下点的像素值 x 右上矩形的面积 + 右上点的像素值 x 左下矩形的面积 + 右下点的像素值 x 左上矩形的面积。

注意，双线性插值的最终结果与执行线性插值的顺序无关，即使先在 y 方向插值后在 x 方向进行插值也会得到相同的结果。

OpenCV 如何实现双线性插值缩放

先上代码：

void resize_linear(float* src, float* dst, int src_width, int src_height, int dst_width, int dst_height, int channels) {
    float scale_x = (float)(src_width) / dst_width;
    float scale_y = (float)(src_height) / dst_height;

    for (int dst_y = 0; dst_y < dst_height; ++dst_y) {
        for (int dst_x = 0; dst_x < dst_width; ++dst_x) {
            float src_y = (dst_y + 0.5) * scale_y - 0.5;
            int src_y_down = floorf(src_y);
            if (src_y_down < 0) {
                src_y_down = 0;
                src_y = src_y_down;
            }
            if (src_y_down >= src_height - 1) {
                src_y_down = src_height - 1;
                src_y = src_y_down;
            }
            int src_y_up = src_y_down + 1;

            float src_x = (dst_x + 0.5) * scale_x - 0.5;
            int src_x_down = floorf(src_x);
            if (src_x_down < 0) {
                src_x_down = 0;
                src_x = src_x_down;
            }
            if (src_x_down >= src_width - 1) {
                src_x_down = src_width - 1;
                src_x = src_x_down;
            }
            int src_x_up = src_x_down + 1;

            float left_top_area = (src_x - src_x_down) * (src_y - src_y_down);
            float right_top_area = (src_x_up - src_x) * (src_y - src_y_down);
            float left_bottom_area = (src_x - src_x_down) * (src_y_up - src_y);
            float right_bottom_area = (src_x_up - src_x) * (src_y_up - src_y);

            if (src_y_up >= src_height) {
                src_y_up = src_height - 1;
                right_top_area = 0.0;
                left_top_area = 0.0;
            }
            if (src_x_up >= src_width) {
                src_x_up = src_width - 1;
                left_bottom_area = 0.0;
                left_top_area = 0.0;
            }

            for (int c = 0; c < channels; c++) {
                dst[dst_y * dst_width * channels + dst_x * channels + c] =
                        src[src_y_down * src_width * channels + src_x_down * channels + c] * right_bottom_area +
                        src[src_y_down * src_width * channels + src_x_up * channels + c] * left_bottom_area +
                        src[src_y_up * src_width * channels + src_x_down * channels + c] * right_top_area +
                        src[src_y_up * src_width * channels + src_x_up * channels + c] * left_top_area;
            }
        }
    }
}

注：这段代码并非 OpenCV 的原始代码，因为原始代码还有更多的抽象与优化，不方便呈现逻辑。

代码的整体逻辑还是比较清晰简单的，不过有一个地方需要注意，就是上述代码的第 8 行和第 21 行，在根据缩放系数求缩放后图中的某个点在原图中的对应位置时，OpenCV 做了一个偏移。也正是因为这个偏移，导致之前手动实现的双线性插值和 OpenCV 的结果不一致。

再来个 CUDA 版本的（naive 实现，没有优化）：

__global__ void resize_linear(float* src, float* dst, int src_width, int src_height, int dst_width, int dst_height, int channels) {
    int dst_x = blockIdx.x * blockDim.x + threadIdx.x;
    int dst_y = blockIdx.y * blockDim.y + threadIdx.y;

    float scale_x = (float)(src_width) / dst_width;
    float scale_y = (float)(src_height) / dst_height;

    if (dst_x < dst_width && dst_y < dst_height) {
        float src_y = (dst_y + 0.5) * scale_y - 0.5;
        int src_y_down = floorf(src_y);
        if (src_y_down < 0) {
            src_y_down = 0;
            src_y = src_y_down;
        }
        if (src_y_down >= src_height - 1) {
            src_y_down = src_height - 1;
            src_y = src_y_down;
        }
        int src_y_up = src_y_down + 1;

        float src_x = (dst_x + 0.5) * scale_x - 0.5;
        int src_x_down = floorf(src_x);
        if (src_x_down < 0) {
            src_x_down = 0;
            src_x = src_x_down;
        }
        if (src_x_down >= src_width - 1) {
            src_x_down = src_width - 1;
            src_x = src_x_down;
        }
        int src_x_up = src_x_down + 1;

        float left_top_area = (src_x - src_x_down) * (src_y - src_y_down);
        float right_top_area = (src_x_up - src_x) * (src_y - src_y_down);
        float left_bottom_area = (src_x - src_x_down) * (src_y_up - src_y);
        float right_bottom_area = (src_x_up - src_x) * (src_y_up - src_y);

        if (src_y_up >= src_height) {
            src_y_up = src_height - 1;
            right_top_area = 0.0;
            left_top_area = 0.0;
        }
        if (src_x_up >= src_width) {
            src_x_up = src_width - 1;
            left_bottom_area = 0.0;
            left_top_area = 0.0;
        }

        for (int c = 0; c < channels; c++) {
            dst[dst_y * dst_width * channels + dst_x * channels + c] =
                    src[src_y_down * src_width * channels + src_x_down * channels + c] * right_bottom_area +
                    src[src_y_down * src_width * channels + src_x_up * channels + c] * left_bottom_area +
                    src[src_y_up * src_width * channels + src_x_down * channels + c] * right_top_area +
                    src[src_y_up * src_width * channels + src_x_up * channels + c] * left_top_area;
        }
    }
}

小结

需要注意的是，基于上面代码实现的 resize 和 OpenCV resize 的结果仍然不是完全一致的，我在多张图片上测试的结果显示，两种方式最多会在某些位置的像素值上差 1。这个差距肉眼是不可识别的，我也在一个目标检测算法上进行了测试，对最终结果也几乎是没有影响的。

有了这个结果对齐的基准实现，后续就可以基于这个代码进行性能优化了。

参考

双线性插值及其在图像中的应用

opencv/resize.cpp at master · opencv/opencv