发表更新CUDA14 分钟读完 (大约2053个字)0次访问

CUDA 实践：滑窗卷积 | CUDA

滑窗卷积（即直接卷积）是实现图像卷积的最直观的方式，但这并不代表性能就差，在通道数较少且宽高较大的某些情况下性能是优于 cuDNN 的。

代码实现

数据拷贝

在本文的 case 中，kernel size 为 3，stride size 为 1，padding size 为 0，block size 为 8x4，如果每个线程负责计算一个输出元素的话，那么每个 block 就需要读取 (8+3-1)x(4+3-1)=10x6 个输入元素。对于位于输入 tensor 边缘的 block，如果凑不成一个完整的 10x6 的块，就和前一个 block 合并在一起，比如 (10x6)+(10x4)=10x10。

为了提高数据拷贝的效率，一个线程需要负责多个元素的拷贝：

相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
int boundary_y = out_h / BLOCK_HEIGHT - 1;
int boundary_x = out_w / BLOCK_WIDTH - 1;
int edge_y = out_h % BLOCK_HEIGHT;
int edge_x = out_w % BLOCK_WIDTH;

// global memory --> shared memory
__shared__ float s_kernel[KERNEL_HEIGHT][KERNEL_WIDTH];
__shared__ float s_in[MALLOC_BLOCK_HEIGHT][MALLOC_BLOCL_WIDTH];
float load_reg[4];

// 当前 block 的起始位置
int begin_pos = block_y * BLOCK_HEIGHT * in_w + block_x * BLOCK_WIDTH;

int single_trans_ele_num = 4;                                // 每个线程一次转移 4 个元素，即 tile 大小为 4（边缘 tile 除外）
int cur_in_block_height = BLOCK_HEIGHT + KERNEL_HEIGHT - 1;  // 当前 block 读入的数据块尺寸
int cur_in_block_width = BLOCK_WIDTH + KERNEL_WIDTH - 1;     // 当前 block 读入的数据块尺寸
int in_tile_thread_per_row;                                  // 需要转移的数据块中每行需要的线程数
int in_tile_row_start;                                       // tile 在 sub-block 中的行坐标
int in_tile_col;                                             // tile 在 sub-block 中的列坐标
int in_tile_row_stride;                                      // 同一个线程两次拷贝需要跨越的行数

// 修正边缘 block 尺寸
if (block_y == boundary_y) {
    cur_in_block_height = BLOCK_HEIGHT + edge_y + KERNEL_HEIGHT - 1;
}
if (block_x == boundary_x) {
    cur_in_block_width = BLOCK_WIDTH + edge_x + KERNEL_WIDTH - 1;
}

in_tile_thread_per_row = cur_in_block_width / single_trans_ele_num;
in_tile_row_start = tid / in_tile_thread_per_row;
in_tile_col = tid % in_tile_thread_per_row * single_trans_ele_num;
in_tile_row_stride = thread_num_per_block / in_tile_thread_per_row;

// copy input block data
if (in_tile_row_start < cur_in_block_height) {  // 超出当前 block 范围的线程不做拷贝操作
    // 这个循环的迭代次数表示同一个线程会执行几次拷贝，即每个线程在执行完自己那次拷贝以后会跨越 in_tile_row_stride 行再执行一次拷贝
    for (int i = 0; i < cur_in_block_height; i += in_tile_row_stride) {
        FETCH_FLOAT4(load_reg[0]) = FETCH_FLOAT4(in[begin_pos + OFFSET(in_tile_row_start + i, in_tile_col, in_w)]);
        s_in[in_tile_row_start + i][in_tile_col + 0] = load_reg[0];
        s_in[in_tile_row_start + i][in_tile_col + 1] = load_reg[1];
        s_in[in_tile_row_start + i][in_tile_col + 2] = load_reg[2];
        s_in[in_tile_row_start + i][in_tile_col + 3] = load_reg[3];
        // 如果 block 的宽度不能被 tile 宽度整除，对于 block 中的边缘 tile 做特殊处理
        if (in_tile_col + 2 * single_trans_ele_num > cur_in_block_width && in_tile_col + 1 * single_trans_ele_num < cur_in_block_width) {
            for (int j = in_tile_col + 1 * single_trans_ele_num; j < cur_in_block_width; ++j) {
                s_in[in_tile_row_start + i][j] = in[begin_pos + OFFSET(in_tile_row_start + i, j, in_w)];
            }
        }
    }
}

在这个 case 中，一个 tile 的大小是 4，边缘 tile 的尺寸可能会更大一些（类似前面对边缘 block 的处理）。如果 block size 设置的比较小而 kernel size 比较大，block 中的所有线程不能一次性把其计算所需的数据搬运完，就需要再进行一次迭代，每个线程再执行一次搬运。每次迭代需要搬运的数据就是前面代码中的 sub-block。

计算输出

在计算输出元素时，每个线程负责 single_calculate_num 个元素，每 single_calculate_num 个元素被称为一个 tile。和数据搬运同理，边缘 tile 需要特殊处理，如果一次处理不完需要进行多次迭代。

在计算输出的过程中，数组 val 用于存储每个 block 中输出的累加中间结果，如下图所示：

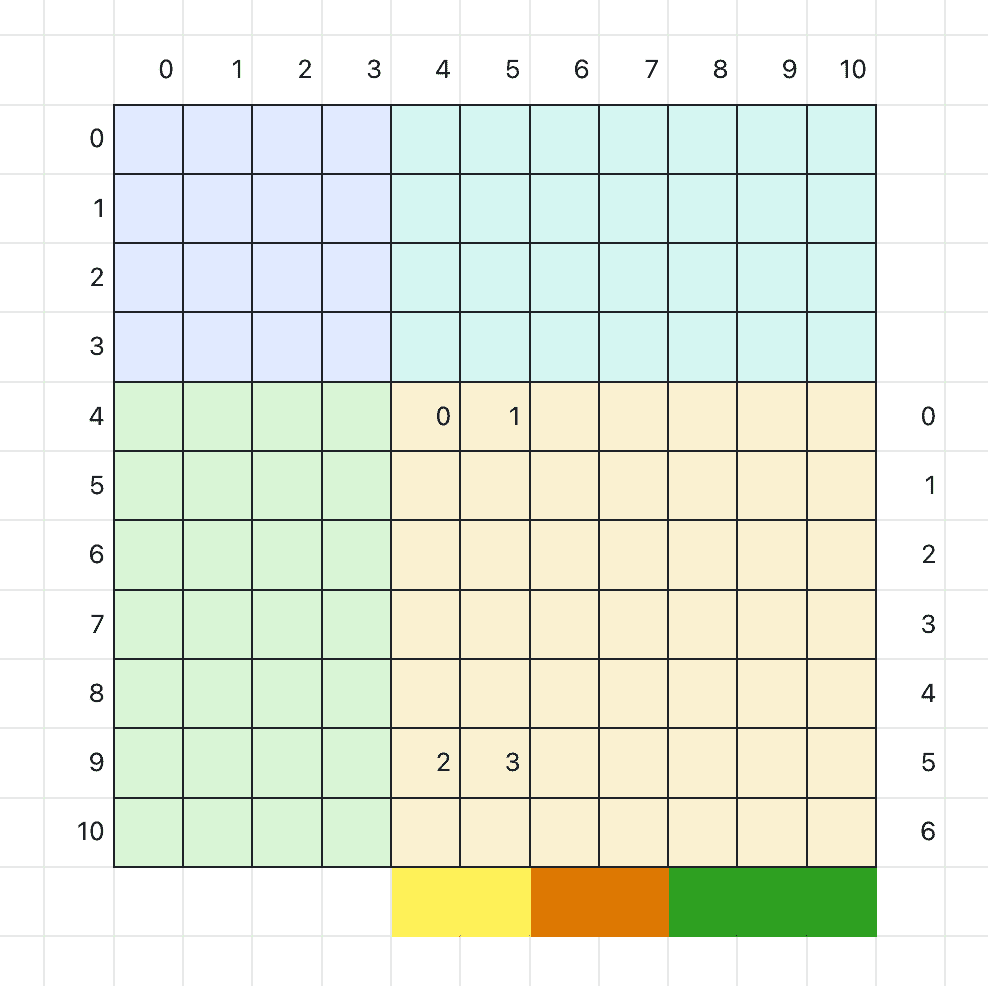
这个图展示一个 11x11 的输出，其中 block size 为 4x4，single_calculate_num 为 2。由于边缘 block 需要特殊处理，所以分块情况就像图中那样分成 4 块。

我们重点看右下角的 block：每一行需要用 3 个线程计算（7=2+2+3），一共需要 3x7=21 个线程完成计算。一个 block 中只有 4x4=16 个线程（本例仅作示例，忽略最小调度单位为 32 个线程这个事实），所以需要两次迭代才能完成这个 block。图中标记了 0,1,2,3 需要的元素就是数组 val，用于存储输出的累加中间结果。可以看出数组 val 的通道数和输出通道数相同，宽取决于 single_calculate_num（需要考虑边缘 tile 的情况），高取决于同一个线程在一个 block 中最多可能迭代的次数。

相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
// 以下变量都是针对输出矩阵而言
int cur_out_block_height = BLOCK_HEIGHT;       // 输出 block 的尺寸
int cur_out_block_width = BLOCK_WIDTH;         // 输出 block 的尺寸
int single_calculate_num = OUTPUT_PER_THREAD;  // 每个线程负责计算的输出元素数目
int out_tile_thread_per_row;                   // 输出 block 每行需要的线程数
int out_tile_row_start;                        // tile 在 sub-block 中的行坐标
int out_tile_col;                              // tile 在 sub-block 中的列坐标
int out_tile_row_stride;                       // 同一个线程两次计算需要跨越的行数（同一个 block 中 sub-block 之间相隔的行数）

// 修正边缘 block 尺寸
if (block_y == boundary_y) {
    cur_out_block_height = BLOCK_HEIGHT + edge_y;
}
if (block_x == boundary_x) {
    cur_out_block_width = BLOCK_WIDTH + edge_x;
}

out_tile_thread_per_row = cur_out_block_width / single_calculate_num;
out_tile_row_start = tid / out_tile_thread_per_row;
out_tile_col = tid % out_tile_thread_per_row * single_calculate_num;
out_tile_row_stride = thread_num_per_block / out_tile_thread_per_row;

float val[MALLOC_TEMP_SIZE];

for (int oc = 0; oc < out_c; ++oc) {
    for (int i = 0; i < MALLOC_TEMP_SIZE; ++i) val[i] = 0;

    for (int ic = 0; ic < in_c; ++ic) {
        for (int i = 0; i < cur_out_block_height && (out_tile_row_start + i) < cur_out_block_height; i += out_tile_row_stride) {
            // 如果 block 的宽度不能被 tile 宽度整除，对于 block 中的边缘 tile 做特殊处理
            int new_single_calculate_num = single_calculate_num;
            if (out_tile_col + 2 * single_calculate_num > cur_out_block_width && out_tile_col + 1 * single_calculate_num < cur_out_block_width) {
                new_single_calculate_num = cur_out_block_width - out_tile_col;  // 对于 block 中的边缘 tile，每个线程负责计算的输出元素个数也会多一点
            }

            for (int j = 0; j < new_single_calculate_num; ++j) {
                int temp_pos = i / out_tile_row_stride * new_single_calculate_num + j;
                for (int ii = 0; ii < KERNEL_HEIGHT; ++ii) {
                    for (int jj = 0; jj < KERNEL_WIDTH; ++jj) {
                        val[temp_pos] += s_in[out_tile_row_start + i + ii][out_tile_col + j + jj] * s_kernel[ii][jj];
                    }
                }
            }
        }

        // 预读取下一个 in channel 和对应 kernel in channel
        ......

        __syncthreads();
    }

    // 预读取下一个 kernel out channel
    ......

    __syncthreads();

    // 写回
    for (int i = 0; i < cur_out_block_height && (out_tile_row_start + i) < cur_out_block_height; i += out_tile_row_stride) {
        // 如果 block 的宽度不能被 tile 宽度整除，对于 block 中的边缘 tile 做特殊处理
        int new_single_calculate_num = single_calculate_num;
        if (out_tile_col + 2 * single_calculate_num > cur_out_block_width && out_tile_col + 1 * single_calculate_num < cur_out_block_width) {
            new_single_calculate_num = cur_out_block_width - out_tile_col;
        }

        for (int j = 0; j < new_single_calculate_num; ++j) {
            int out_pos = oc * out_h * out_w + block_y * BLOCK_HEIGHT * out_w + block_x * BLOCK_WIDTH + OFFSET(out_tile_row_start + i, out_tile_col + j, out_w);
            int temp_pos = i / out_tile_row_stride * new_single_calculate_num + j;
            out[out_pos] = val[temp_pos];
        }
    }

    // 预读取下一个 in channel
    ......
}

性能测试

正如前面所提到的，上述代码在通道数较少且宽高较大的某些情况下性能是优于 cuDNN 的（NVIDIA A10）：

channel number, kernel size, input size cuDNN 手写
3, 6, 1000 0.90 ms 0.53 ms
3, 3, 1000 0.25 ms 0.46 ms
8, 6, 1000 2.36 ms 6.08 ms

cuDNN 在大 kernel 场景下的优化做的不好。另外手写版本在输入通道这个维度上的访存连续性较差，所以在通道数变多以后性能会劣化比较严重。

完整代码在 zh0ngtian/cuda_learning。

TODO

  • 修复部分输入尺寸下访存越界的问题
  • 解决 bank conflict

参考

CUDA卷积算子手写详细实现

CUDA 实践：滑窗卷积 | CUDA

http://www.zh0ngtian.tech/posts/7da703ee.html

作者

zhongtian

发布于

2023-12-02

更新于

2024-01-06

许可协议

评论

×